En esta entrada vamos a ensayar distintos algoritmos en C++ para el cálculo rápido de la mediana un microprocesador como Arduino. El interés que tenemos en el cálculo de la mediana es que, en ciertas aplicaciones, resulta un mejor estadístico frente a otros como la media.
En la entrada muestreo múltiple vimos que para mejorar la precisión en adquisición de datos la práctica habitual es realizar varias mediciones y combinar los distintos elementos en algún cálculo.
El primer candidato que seguramente nos viene a la cabeza es emplear la media, como veremos en su momento al hacer un filtro de media móvil. Sin embargo, la media tiene el problema de verse afectada por el ruido y especialmente por puntos espurios.
Imaginemos que tomamos diez mediciones de un sensor, y obtenemos 9 valores entre de 19.7 a 19.9. Pero una de las mediciones da un punto anómalo con un valor de 1000. Un único valor ha hecho que la media se vaya a casi 58, arruinando toda la serie.
Si queréis un ejemplo más cotidiano y cercano, 10 personas en una habitación cobran de media 1000 euros. Pero puede ser que 9 estén cobrando 100 euros y el último 9100. Ese es el problema de la media.
En estas circunstancias el uso de un estadístico como la mediana puede ser más representativo de la tendencia. De hecho la “estadística robusta”, una representación alternativa a la estadística clásica centrada en la robustez de los datos, emplea la mediana en lugar de la media como indicador de tendencia.
Uno de los motivos por los que la mediana tradicionalmente ha sido relegada por la media como indicador no es su mayor significación estadística si no que, simplemente, esta última es sencilla y rápida de calcular. Además, es una función que podemos manipular matemáticamente y derivar para emplear en soluciones de optimización.
En oposición, el cálculo de la mediana es un proceso costoso. Además, no es una función con la que podamos operar y no es derivable. Sin embargo, la mediana tiene la ventaja de ser más robusta a la aparición de ruido, especialmente de puntos espurios.
Esto hace que la mediana sea muy común en filtros de adquisición, donde muestra un mejor comportamiento especialmente en filtrado de ruido de tipo sal y pimienta. Veremos esto al aplicar el filtrado de mediana.
Comúnmente se considera que el cálculo de la mediana requiere ordenar los elementos de la muestra y tomar el término medio. Sin embargo, existen algoritmos más eficientes para el cálculo de la mediana.
Aquí vamos a ensayar tres algoritmos distintos con dos muestras de 100 y 500 elementos en un Arduino Nano 16Mhz. Como ya dijimos en la entrada de QuickSort, por sus limitaciones no resulta la máquina más adecuada para cálculos, y si necesitamos estos cálculos deberíamos plantearnos un procesador superior. ¡Pero realizar las pruebas con 10 elementos sería aburrido!
Algoritmo QuickSort
El caso base de estudio es realizar la ordenación del vector de entrada y tomar el punto medio. Para ello usaremos el algoritmo QuickSort que vimos en la última entrada por ser uno de los algoritmos más rápidos para ordenar un vector.
int values100[] = { 3, 53, 70, 56, 18, 85, 27, 14, 37, 94, 9, 55, 40, 60, 52, 61, 15, 65, 13, 8, 57, 97, 69, 4, 35, 82, 22, 73, 59, 68, 78, 24, 21, 36, 71, 80, 74, 39, 17, 12, 29, 76, 49, 51, 30, 90, 88, 2, 84, 50, 62, 28, 77, 43, 5, 16, 58, 26, 32, 34, 1, 75, 66, 95, 38, 89, 67, 87, 100, 54, 92, 81, 25, 83, 46, 33, 23, 45, 96, 99, 79, 48, 11, 31, 7, 6, 19, 91, 93, 44, 47, 98, 86, 41, 63, 20, 72, 10, 42, 64 };
int values100Length = sizeof(values100) / sizeof(int);
int values500[] = { 404, 267, 446, 214, 45, 149, 475, 496, 233, 78, 248, 307, 95, 431, 479, 445, 181, 370, 458, 476, 371, 122, 231, 74, 8, 392, 355, 397, 426, 125, 15, 159, 172, 369, 441, 318, 203, 399, 249, 225, 457, 351, 462, 184, 384, 100, 265, 244, 32, 499, 448, 29, 412, 447, 110, 473, 12, 414, 311, 301, 56, 84, 243, 378, 210, 217, 165, 10, 79, 374, 337, 52, 373, 395, 30, 126, 116, 280, 313, 474, 157, 6, 467, 459, 381, 129, 482, 13, 179, 167, 72, 68, 112, 194, 205, 97, 342, 142, 4, 418, 22, 440, 430, 364, 82, 483, 158, 198, 124, 259, 20, 312, 241, 254, 456, 361, 5, 245, 281, 376, 461, 274, 219, 348, 235, 23, 328, 2, 136, 291, 455, 302, 107, 415, 393, 43, 427, 211, 223, 168, 340, 87, 286, 133, 228, 354, 182, 204, 67, 419, 63, 270, 463, 60, 49, 358, 362, 102, 330, 242, 406, 108, 221, 83, 300, 363, 166, 290, 389, 436, 263, 34, 487, 377, 106, 491, 434, 257, 207, 417, 47, 379, 343, 500, 339, 403, 390, 61, 495, 262, 128, 132, 293, 94, 69, 143, 279, 375, 421, 109, 237, 310, 432, 218, 161, 150, 470, 200, 121, 464, 494, 443, 466, 252, 33, 105, 173, 344, 275, 388, 289, 333, 409, 452, 118, 315, 489, 283, 433, 442, 439, 114, 334, 229, 304, 175, 253, 216, 236, 256, 70, 169, 321, 365, 405, 366, 91, 380, 37, 212, 429, 336, 141, 308, 90, 492, 31, 460, 324, 387, 156, 120, 24, 183, 401, 81, 51, 288, 3, 367, 246, 498, 39, 386, 36, 192, 352, 292, 451, 294, 50, 326, 345, 76, 319, 360, 335, 306, 48, 239, 309, 468, 331, 226, 385, 347, 295, 44, 89, 497, 438, 332, 297, 346, 25, 199, 485, 469, 55, 402, 193, 284, 264, 135, 7, 14, 53, 197, 88, 201, 232, 258, 234, 481, 255, 9, 186, 59, 162, 18, 98, 93, 154, 73, 327, 278, 230, 131, 145, 26, 465, 103, 220, 19, 316, 177, 407, 146, 42, 153, 144, 99, 117, 28, 62, 148, 282, 453, 137, 208, 424, 450, 1, 477, 164, 368, 119, 21, 396, 127, 484, 277, 130, 437, 111, 206, 64, 391, 322, 151, 372, 188, 191, 57, 160, 383, 411, 180, 104, 16, 147, 170, 285, 350, 394, 71, 190, 54, 251, 261, 272, 320, 196, 338, 425, 227, 178, 420, 123, 174, 276, 480, 138, 80, 486, 454, 490, 435, 400, 77, 444, 323, 140, 171, 139, 195, 260, 314, 92, 17, 449, 222, 187, 296, 96, 40, 58, 423, 152, 11, 269, 359, 329, 422, 410, 155, 250, 101, 240, 213, 478, 273, 189, 27, 471, 356, 416, 238, 35, 41, 398, 113, 268, 46, 215, 85, 488, 325, 163, 202, 247, 341, 382, 299, 185, 176, 224, 472, 115, 349, 271, 303, 287, 408, 428, 65, 134, 75, 305, 66, 298, 357, 38, 266, 353, 209, 493, 317, 86, 413 };
int values500Length = sizeof(values500) / sizeof(int);
void setup()
{
Serial.begin(115200);
Serial.println("Mediana 100 valores");
long timeCount = micros();
QuickSortAsc(values100, 0, values100Length - 1);
timeCount = micros() - timeCount;
Serial.println(values100[values100Length/2-1]);
Serial.println();
Serial.print(timeCount);
Serial.println("us");
Serial.println("");
Serial.println("Mediana 500 valores");
timeCount = micros();
QuickSortAsc(values500, 0, values500Length - 1);
timeCount = micros() - timeCount;
Serial.println(values500[values500Length/2-1]);
Serial.println();
Serial.print(timeCount);
Serial.println("us");
}
void loop()
{
}
void QuickSortAsc(int* arr, const int left, const int right)
{
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
while (i <= j)
{
while (arr[i]<pivot) i++;
while (arr[j]>pivot) j--;
if (i <= j)
{
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
if (left<j)
QuickSortAsc(arr, left, j);
if (i<right)
QuickSortAsc(arr, i, right);
}Estos son los resultados.
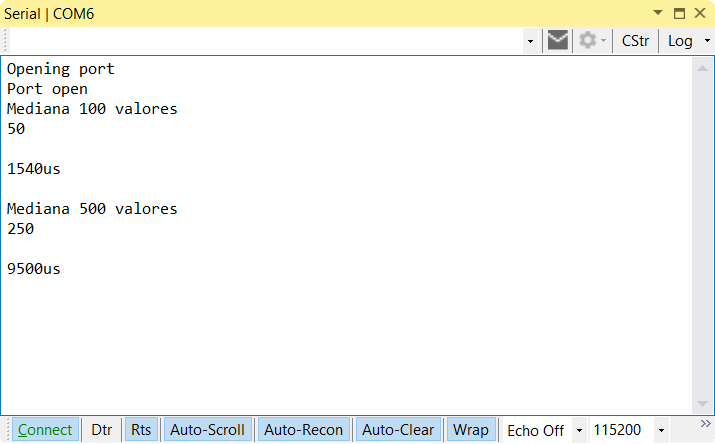
Lógicamente, los tiempos idénticos a los obtenidos con en la entrada de QuickSort, 1540us para la muestra de 100 elementos, y 9500us para la muestra de 500 elementos.
Algoritmo QuickSelect
El algoritmo QuickSelect que permite obtener el k-ésimo elemento de una lista. Está basado en QuickSort desarrollado por el mismo autor (Tony Hoare) y comparte el sistema de partición y pivotaje. Sin embargo, al prescindir de tener que ordenar toda la lista el orden de QuickSelect baja de O(n log n) de QuickSort a O(n) en QuickSelect, manteniendo en el peor de los casos O(n2).
#define ELEM_SWAP(a,b) { register float t=(a);(a)=(b);(b)=t; }
int values100[] = { 3, 53, 70, 56, 18, 85, 27, 14, 37, 94, 9, 55, 40, 60, 52, 61, 15, 65, 13, 8, 57, 97, 69, 4, 35, 82, 22, 73, 59, 68, 78, 24, 21, 36, 71, 80, 74, 39, 17, 12, 29, 76, 49, 51, 30, 90, 88, 2, 84, 50, 62, 28, 77, 43, 5, 16, 58, 26, 32, 34, 1, 75, 66, 95, 38, 89, 67, 87, 100, 54, 92, 81, 25, 83, 46, 33, 23, 45, 96, 99, 79, 48, 11, 31, 7, 6, 19, 91, 93, 44, 47, 98, 86, 41, 63, 20, 72, 10, 42, 64 };
int values100Length = sizeof(values100) / sizeof(int);
int values500[] = { 404, 267, 446, 214, 45, 149, 475, 496, 233, 78, 248, 307, 95, 431, 479, 445, 181, 370, 458, 476, 371, 122, 231, 74, 8, 392, 355, 397, 426, 125, 15, 159, 172, 369, 441, 318, 203, 399, 249, 225, 457, 351, 462, 184, 384, 100, 265, 244, 32, 499, 448, 29, 412, 447, 110, 473, 12, 414, 311, 301, 56, 84, 243, 378, 210, 217, 165, 10, 79, 374, 337, 52, 373, 395, 30, 126, 116, 280, 313, 474, 157, 6, 467, 459, 381, 129, 482, 13, 179, 167, 72, 68, 112, 194, 205, 97, 342, 142, 4, 418, 22, 440, 430, 364, 82, 483, 158, 198, 124, 259, 20, 312, 241, 254, 456, 361, 5, 245, 281, 376, 461, 274, 219, 348, 235, 23, 328, 2, 136, 291, 455, 302, 107, 415, 393, 43, 427, 211, 223, 168, 340, 87, 286, 133, 228, 354, 182, 204, 67, 419, 63, 270, 463, 60, 49, 358, 362, 102, 330, 242, 406, 108, 221, 83, 300, 363, 166, 290, 389, 436, 263, 34, 487, 377, 106, 491, 434, 257, 207, 417, 47, 379, 343, 500, 339, 403, 390, 61, 495, 262, 128, 132, 293, 94, 69, 143, 279, 375, 421, 109, 237, 310, 432, 218, 161, 150, 470, 200, 121, 464, 494, 443, 466, 252, 33, 105, 173, 344, 275, 388, 289, 333, 409, 452, 118, 315, 489, 283, 433, 442, 439, 114, 334, 229, 304, 175, 253, 216, 236, 256, 70, 169, 321, 365, 405, 366, 91, 380, 37, 212, 429, 336, 141, 308, 90, 492, 31, 460, 324, 387, 156, 120, 24, 183, 401, 81, 51, 288, 3, 367, 246, 498, 39, 386, 36, 192, 352, 292, 451, 294, 50, 326, 345, 76, 319, 360, 335, 306, 48, 239, 309, 468, 331, 226, 385, 347, 295, 44, 89, 497, 438, 332, 297, 346, 25, 199, 485, 469, 55, 402, 193, 284, 264, 135, 7, 14, 53, 197, 88, 201, 232, 258, 234, 481, 255, 9, 186, 59, 162, 18, 98, 93, 154, 73, 327, 278, 230, 131, 145, 26, 465, 103, 220, 19, 316, 177, 407, 146, 42, 153, 144, 99, 117, 28, 62, 148, 282, 453, 137, 208, 424, 450, 1, 477, 164, 368, 119, 21, 396, 127, 484, 277, 130, 437, 111, 206, 64, 391, 322, 151, 372, 188, 191, 57, 160, 383, 411, 180, 104, 16, 147, 170, 285, 350, 394, 71, 190, 54, 251, 261, 272, 320, 196, 338, 425, 227, 178, 420, 123, 174, 276, 480, 138, 80, 486, 454, 490, 435, 400, 77, 444, 323, 140, 171, 139, 195, 260, 314, 92, 17, 449, 222, 187, 296, 96, 40, 58, 423, 152, 11, 269, 359, 329, 422, 410, 155, 250, 101, 240, 213, 478, 273, 189, 27, 471, 356, 416, 238, 35, 41, 398, 113, 268, 46, 215, 85, 488, 325, 163, 202, 247, 341, 382, 299, 185, 176, 224, 472, 115, 349, 271, 303, 287, 408, 428, 65, 134, 75, 305, 66, 298, 357, 38, 266, 353, 209, 493, 317, 86, 413 };
int values500Length = sizeof(values500) / sizeof(int);
void setup()
{
Serial.begin(115200);
Serial.println("Mediana 100 valores");
long timeCount = micros();
QuickSelectMedian(values100, values100Length);
timeCount = micros() - timeCount;
Serial.println(values100[values100Length/2-1]);
Serial.println();
Serial.print(timeCount);
Serial.println("us");
Serial.println("");
Serial.println("Mediana 500 valores");
timeCount = micros();
QuickSelectMedian(values500, values500Length);
timeCount = micros() - timeCount;
Serial.println(values500[values500Length/2-1]);
Serial.println();
Serial.print(timeCount);
Serial.println("us");
}
void loop()}
int QuickSelectMedian(int arr[], uint16_t n)
{
uint16_t low, high;
uint16_t median;
uint16_t middle, ll, hh;
low = 0; high = n - 1; median = (low + high) / 2;
for (;;)
{
if (high <= low)
return arr[median];
if (high == low + 1)
{
if (arr[low] > arr[high])
ELEM_SWAP(arr[low], arr[high]);
return arr[median];
}
middle = (low + high) / 2;
if (arr[middle] > arr[high])
ELEM_SWAP(arr[middle], arr[high]);
if (arr[low] > arr[high])
ELEM_SWAP(arr[low], arr[high]);
if (arr[middle] > arr[low])
ELEM_SWAP(arr[middle], arr[low]);
ELEM_SWAP(arr[middle], arr[low + 1]);
ll = low + 1;
hh = high;
for (;;)
{
do ll++; while (arr[low] > arr[ll]);
do hh--; while (arr[hh] > arr[low]);
if (hh < ll)
break;
ELEM_SWAP(arr[ll], arr[hh]);
}
ELEM_SWAP(arr[low], arr[hh]);
if (hh <= median)
low = ll;
if (hh >= median)
high = hh - 1;
}
return arr[median];
}Los resultados son los siguientes.
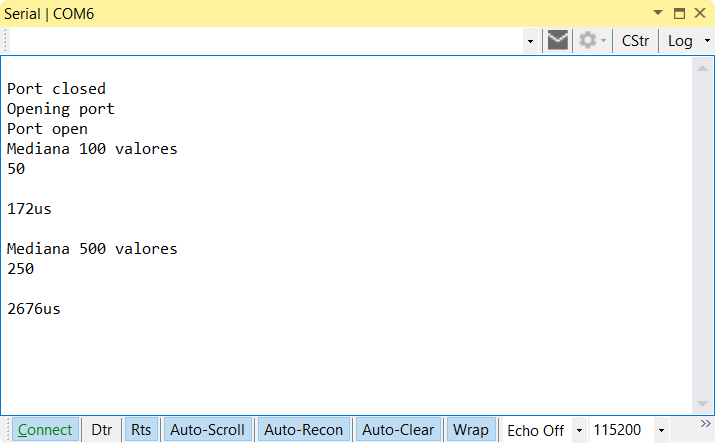
El tiempo para la muestra de 100 elementos con QuickSelect es 172us, 8.95 veces más rápido que ordenar la lista. En el caso de la muestra de 500 elementos el tiempo es de 2676us, 3.55 veces más rápido que realizar la ordenación de la lista.
Algoritmo Wirth
El algoritmo desarrollado por Niklaus Wirth es una variación del algoritmo QuickSelect de Hoare que admite una implementación más sencilla y eficiente. Fue presentado en 1976 en el libro “Algorithms + data structures = programs”
int values100[] = { 3, 53, 70, 56, 18, 85, 27, 14, 37, 94, 9, 55, 40, 60, 52, 61, 15, 65, 13, 8, 57, 97, 69, 4, 35, 82, 22, 73, 59, 68, 78, 24, 21, 36, 71, 80, 74, 39, 17, 12, 29, 76, 49, 51, 30, 90, 88, 2, 84, 50, 62, 28, 77, 43, 5, 16, 58, 26, 32, 34, 1, 75, 66, 95, 38, 89, 67, 87, 100, 54, 92, 81, 25, 83, 46, 33, 23, 45, 96, 99, 79, 48, 11, 31, 7, 6, 19, 91, 93, 44, 47, 98, 86, 41, 63, 20, 72, 10, 42, 64 };
int values100Length = sizeof(values100) / sizeof(int);
int values500[] = { 404, 267, 446, 214, 45, 149, 475, 496, 233, 78, 248, 307, 95, 431, 479, 445, 181, 370, 458, 476, 371, 122, 231, 74, 8, 392, 355, 397, 426, 125, 15, 159, 172, 369, 441, 318, 203, 399, 249, 225, 457, 351, 462, 184, 384, 100, 265, 244, 32, 499, 448, 29, 412, 447, 110, 473, 12, 414, 311, 301, 56, 84, 243, 378, 210, 217, 165, 10, 79, 374, 337, 52, 373, 395, 30, 126, 116, 280, 313, 474, 157, 6, 467, 459, 381, 129, 482, 13, 179, 167, 72, 68, 112, 194, 205, 97, 342, 142, 4, 418, 22, 440, 430, 364, 82, 483, 158, 198, 124, 259, 20, 312, 241, 254, 456, 361, 5, 245, 281, 376, 461, 274, 219, 348, 235, 23, 328, 2, 136, 291, 455, 302, 107, 415, 393, 43, 427, 211, 223, 168, 340, 87, 286, 133, 228, 354, 182, 204, 67, 419, 63, 270, 463, 60, 49, 358, 362, 102, 330, 242, 406, 108, 221, 83, 300, 363, 166, 290, 389, 436, 263, 34, 487, 377, 106, 491, 434, 257, 207, 417, 47, 379, 343, 500, 339, 403, 390, 61, 495, 262, 128, 132, 293, 94, 69, 143, 279, 375, 421, 109, 237, 310, 432, 218, 161, 150, 470, 200, 121, 464, 494, 443, 466, 252, 33, 105, 173, 344, 275, 388, 289, 333, 409, 452, 118, 315, 489, 283, 433, 442, 439, 114, 334, 229, 304, 175, 253, 216, 236, 256, 70, 169, 321, 365, 405, 366, 91, 380, 37, 212, 429, 336, 141, 308, 90, 492, 31, 460, 324, 387, 156, 120, 24, 183, 401, 81, 51, 288, 3, 367, 246, 498, 39, 386, 36, 192, 352, 292, 451, 294, 50, 326, 345, 76, 319, 360, 335, 306, 48, 239, 309, 468, 331, 226, 385, 347, 295, 44, 89, 497, 438, 332, 297, 346, 25, 199, 485, 469, 55, 402, 193, 284, 264, 135, 7, 14, 53, 197, 88, 201, 232, 258, 234, 481, 255, 9, 186, 59, 162, 18, 98, 93, 154, 73, 327, 278, 230, 131, 145, 26, 465, 103, 220, 19, 316, 177, 407, 146, 42, 153, 144, 99, 117, 28, 62, 148, 282, 453, 137, 208, 424, 450, 1, 477, 164, 368, 119, 21, 396, 127, 484, 277, 130, 437, 111, 206, 64, 391, 322, 151, 372, 188, 191, 57, 160, 383, 411, 180, 104, 16, 147, 170, 285, 350, 394, 71, 190, 54, 251, 261, 272, 320, 196, 338, 425, 227, 178, 420, 123, 174, 276, 480, 138, 80, 486, 454, 490, 435, 400, 77, 444, 323, 140, 171, 139, 195, 260, 314, 92, 17, 449, 222, 187, 296, 96, 40, 58, 423, 152, 11, 269, 359, 329, 422, 410, 155, 250, 101, 240, 213, 478, 273, 189, 27, 471, 356, 416, 238, 35, 41, 398, 113, 268, 46, 215, 85, 488, 325, 163, 202, 247, 341, 382, 299, 185, 176, 224, 472, 115, 349, 271, 303, 287, 408, 428, 65, 134, 75, 305, 66, 298, 357, 38, 266, 353, 209, 493, 317, 86, 413 };
int values500Length = sizeof(values500) / sizeof(int);
#define ELEM_SWAP(a,b) { register float t=(a);(a)=(b);(b)=t; }
#define median(a,n) wirth_kth_smallest(a,n,(((n)&1)?((n)/2):(((n)/2)-1)))
void setup()
{
Serial.begin(115200);
int med;
Serial.println("Mediana 100 valores");
long timeCount = micros();
med = median(values100, values100Length);
timeCount = micros() - timeCount;
Serial.println(med);
Serial.println();
Serial.print(timeCount);
Serial.println("us");
Serial.println("");
Serial.println("Mediana 500 valores");
timeCount = micros();
med = median(values500, values500Length);
timeCount = micros() - timeCount;
Serial.println(med);
Serial.println();
Serial.print(timeCount);
Serial.println("us");
}
void loop()
{
}
int wirth_kth_smallest(int a[], int n, int k)
{
int i, j, l, m;
int x;
l = 0;
m = n - 1;
while (l<m)
{
x = a[k];
i = l;
j = m;
do {
while (a[i]<x) i++;
while (x<a[j]) j--;
if (i <= j)
{
ELEM_SWAP(a[i], a[j]);
i++;
j--;
}
} while (i <= j);
if (j<k) l = i;
if (k<i) m = j;
}
return a[k];
}Los resultados son los siguientes.
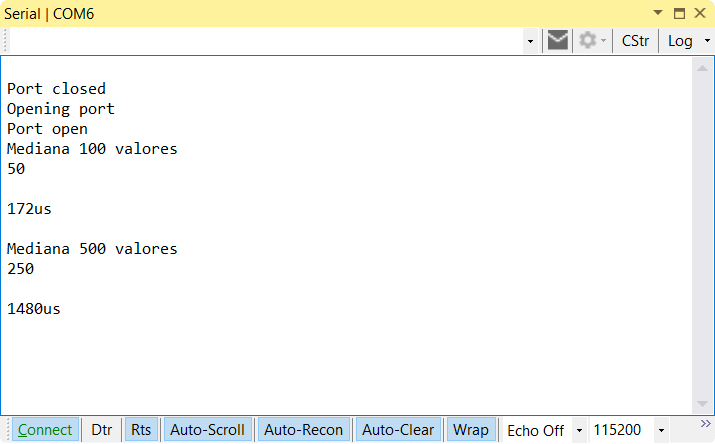
El tiempo para la muestra de 100 elementos es de 172us, 8.95 veces más rápido que QuickSort y exactamente igual que el algoritmo QuickSelect. En el caso de la muestra de 500 elementos es de 1480us, 6.42 veces más rápido que ordenar la lista, y 1.80 veces más rápido que QuickSelect.
QuickMedian en una librería
¿Y si lo metemos en una librería para que sea más cómodo de usar? Por supuesto que sí, aquí tenéis los algoritmos en una librería de QuickMedian para Arduino. ¡A disfrutar!
Descarga el código
Todo el código de esta entrada está disponible para su descarga en Github.

