Llevamos unas entradas hablando sobre cómo reducir el ruido en mediciones mediante el muestreo múltiple y la aplicación de filtros como el filtro de media móvil.
En esta entrada vamos a ver el filtro exponencial EMA (Exponential Moving Average). El filtrado exponencial EMA es uno de los más empleados en electrónica digital por sus buenos resultados unidos a una increíblemente sencilla y eficiente implementación.
El filtro EMA consiste en obtener un valor filtrado a partir de una medición mediante la aplicación de la siguiente expresión
Siendo An el valor filtrado, An-1 el valor filtrado anterior, M es el valor muestreado de la señal a filtrar, y alpha es un factor entre 0 y 1.
Por tanto, el filtro EMA presenta un aporte de información “nueva” a través de la medición M, y un efecto de suavizado basado en la memoria que aporta el valor filtrado anterior An-1. El resultado de un filtro exponencial EMA es una señal suavizada donde la cantidad de suavizado depende del factor alpha, como analizaremos posteriormente.
Las ventajas en cuanto a sencillez y eficiencia computacional son evidentes. El cálculo requiere una única instrucción sencilla. En cuanto a requisitos de memoria necesitamos almacenar únicamente el valor filtrado anterior. Esto supone una gran ventaja computacional frente a otros filtros que requieren guardar N valores y ejecutar cálculos sobre todos ellos.
Filtro paso bajo
Como todos los filtros que suavizan una señal (no es exclusivo del filtro EMA) podemos emplear el filtro exponencial como un filtro paso bajo, es decir, un algoritmo que (idealmente) deja pasar los componentes frecuenciales inferiores a una frecuencia de corte.
Podemos emplear el filtro paso bajo para eliminar el ruido de alta frecuencia superpuesto a la señal, lo que podemos emplear para mejorar la medición de sensores y las comunicaciones, entre otros usos.
Lamentablemente, ningún filtro real es perfecto y los filtros que podemos generar en la realidad tienen limitaciones que lo alejan del comportamiento ideal.
Además, aunque pudiéramos genera un filtro ideal tampoco significa que pudiéramos eliminar por completo el ruido, ya que ciertas frecuencias pueden superponerse con las frecuencias de interés de la propia señal (las variaciones reales de la señal).
Filtro paso alto
Aunque menos frecuentes, también es posible obtener un filtro paso alto, es decir, eliminar las frecuencias inferiores a una frecuencia de corte.
Un filtro de paso alto puede servir, por ejemplo, para eliminar digitalmente el componente de corriente continua de una señal (bias), variaciones lentas comparadas con la frecuencia de interés, detección de cambios bruscos en la señal, entre otros.
Si pudiéramos construir un filtro de paso bajo ideal, para obtener el filtro de paso alto únicamente tenemos que restar la señal tras el filtro paso bajo a la señal original.
Por descontado, en el mundo real también es imposible construir un filtro de paso alto ideal. En el caso (muy frecuente) de construir el filtro de paso alto a partir de un filtro de paso bajo, las limitaciones que obtendremos son el resultado de las del filtro paso bajo empleado.
Influencia del factor Alpha
El factor Alpha condiciona el comportamiento del filtro exponencial y está relacionado con la frecuencia de corte del filtro. Sin embargo una relación sencilla no es siempre posible ya que depende del tiempo de muestreo de nuestro sistema que, en principio, es desconocido y posiblemente variable entre ciclos.
De forma cuantitativa:
- Un valor Alpha = 1 proporciona la señal sin filtrar, ya que prescinde del efecto filtrado que proporciona la medición anterior.
- Un valor de Alpha = 0 provoca que el valor filtrado siempre sea 0, ya que prescinde la información nueva que aporta la medición al sistema.
Disminuir el factor Alpha aumenta el suavizado de la señal, pero a costa de introducir consecuencias también negativas. Por un lado, podemos eliminar componentes frecuenciales que realmente nos fueran de interés, clasificando como ruido algo que realmente era una variación real de la señal.
Por otro lado, disminuir el factor Alpha aumenta el tiempo de respuesta del sistema, es decir, el tiempo que tarda el sistema en estabilizarse ante una entrada constante. Esto se traduce en la introducción de un retraso entre la señal original y la señal filtrada.
Lógicamente el valor de Alpha adecuado dependerá de las características de nuestro sistema, de la señal muestreada, y el ruido que queramos eliminar. En principio, deberemos ajustar el valor para que resulte adecuado a nuestro montaje, siendo valores habituales 0.2-0.6.
Resultados filtro paso bajo y paso alto
Para ilustrar la variación del comportamiento del filtro paso bajo y paso alto vamos a ver el efecto para distintos valores de Alpha ante una misma señal simulada. La señal tiene un componente senoidal principal y superpuesto ruidos de distintas frecuencias.
Aquí tenemos el resultado de filtro paso bajo para un valor de Alpha de 0.6 (un valor bastante común en el mundo real). Vemos que se ha eliminado una parte del ruido de alta frecuencia, y conservado la mayor parte de la señal.
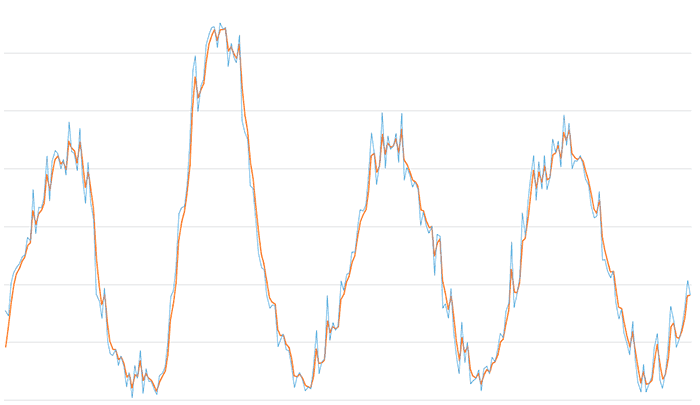
El resultado de filtro paso bajo para un valor de 0.2. El suavizado se ha incrementado y hemos eliminado todo el ruido de alta frecuencia. Por contra, el retraso de la señal filtrada empieza a hacerse evidente.
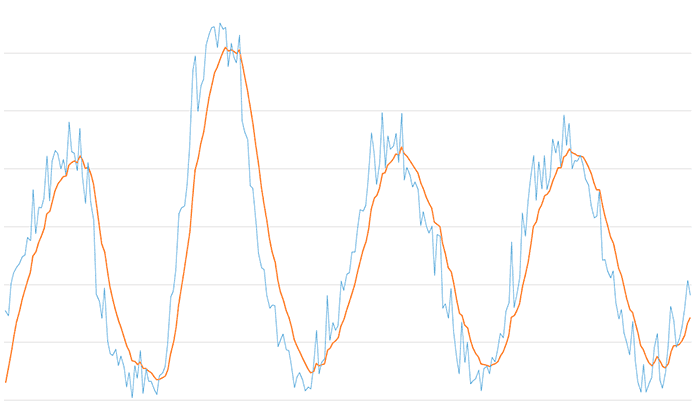
Y el resultado del filtro paso bajo para un valor bajo de 0.05. Se ha eliminado todos los componentes de la señal excepto el principal, pero a cambio tenemos un retraso muy importante de la señal filtrada.
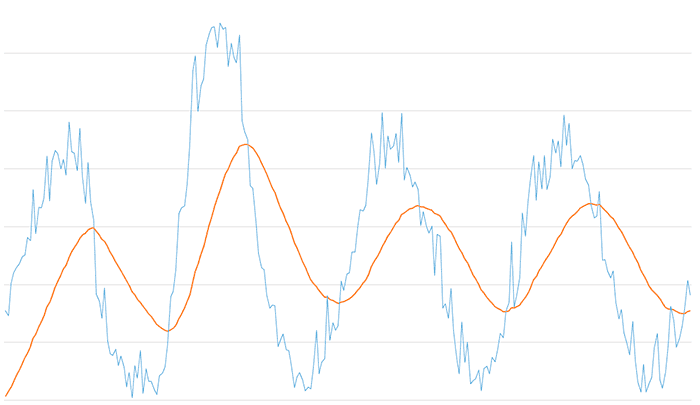
Respecto al filtro de paso alto, aquí tenemos el resultado para el filtro paso alto para un valor de Alpha de 0.6. Vemos que se elimina las componentes de baja frecuencia de la señal, dejando las variaciones más rápidas, que aparecen centradas en el eje Y0.
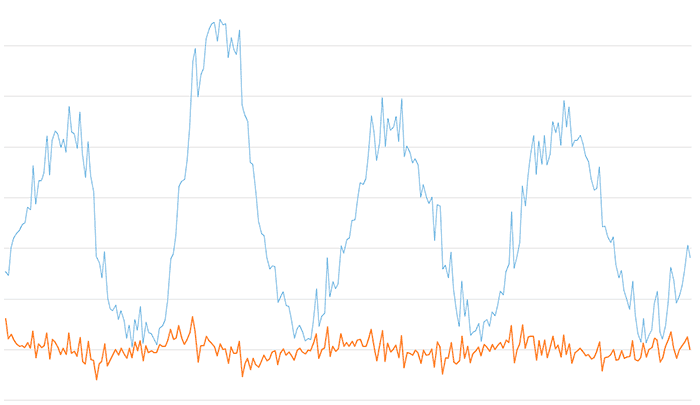
Y aquí el resultado del filtro de paso alto para un valor de Alpha de 0.025. Observamos que se conserva la forma de la señal original, pero pasado un cierto transitorio se ha eliminado por completo el bias de la señal, que ahora aparece centrada en el origen.
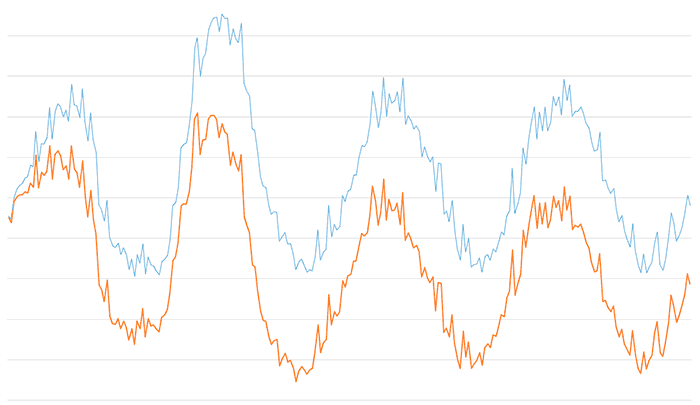
Como veis tenemos una gran variedad de comportamientos con el mismo filtro y da lugar a resultados muy interesantes, desde suavizado de señal y filtrado de ruido de alta frecuencia con el filtro paso bajo, a eliminación del bias u obtención de frecuencias principales con el filtro paso alto.
¿Por qué funciona el filtro EMA?
Resulta habitual encontrar bibliografía y proyectos donde se emplea un filtrado exponencial EMA. Lo que no es tan frecuente de encontrar es explicar por qué funciona un filtro EMA.
Así que ¿Por qué esta sencilla operación es capaz de filtrar el ruido de una señal?
Atención, a continuación llega un apartado de uso demostraciones matemáticas “denso”. Si no te gustan las matemáticas, o no te apetece calentarte la cabeza ahora mismo, puedes pasar al siguiente apartado.

En realidad el filtro exponencial EMA es un caso particular de media de pesos ponderados, es decir, un cálculo de media en la que cada uno de los elementos Xi dispone de un factor Wi que pondera su efecto en el cálculo global de la media.
¿Cómo es que la formulación que hemos visto anteriormente para el filtro EMA puede deducirse de un caso particular de media ponderada?
Partamos de una expresión genérica para obtener una serie de valores filtrados Ai a partir de una serie de mediciones Mi, sujeta a dos parámetros alpha y beta.
Analizando lo que ocurre al emplear esta expresión a la serie de mediciones
Generalizando podemos escribir,
Por tanto, el próximo valor filtrado es la suma de todas las mediciones anteriores ponderados por un factor exponencial beta (que da origen al nombre del filtro) y escalado con un factor alpha.
La teoría indica que la media calcula el efecto de todas las mediciones anteriores, aunque el factor beta^n haga que su efecto sea reducido. No obstante en el mundo real, a consecuencia del redondeo, la contribución de los términos es nula pasada unas cuantas iteraciones.
¿De donde viene las restricciones de que tanto alpha como beta deben ser menor que 1, y que ambos sumados deben ser igual a 1? Bueno, ¿supongo que a estas alturas decir que porque resulta intuitivo no os satisface no? Ya que estoy metido en harina vamos a llegar hasta el final.
En primer lugar, dado que el valor filtrado se obtiene a partir de una serie de tipo geométrico se deduce que, salvo que todas las mediciones sean igual a 0, cualquier factor de beta mayor que 1 provocará una señal general retroalimente rápidamente para tender a infinito.
Por otro lado, valores de beta negativos producirían soluciones oscilantes. Por tanto, se deduce que para obtener una estabilidad beta debe estar comprendido entre 0 y 1.
Para comprobar la relación entre alpha y beta, supongamos como simplificación que introducimos como entrada un valor constante C. Es razonable esperar que el valor filtrado obtenido sea igualmente C. (menudo filtro sería si introducimos constantemente, por ejemplo, 10, y el nos diera 8, o 12 ¿no?)
Siendo B < 1 la expresión anterior se simplifica en
Que finalmente se reduce a,
Con lo que las restricciones sobre alpha y beta quedan explicadas. También podríais haber aceptado la respuesta de que desde el punto de vista de una formulación variacional del problema las restricciones sobre alpha y beta permiten el invariante del funcional de energía. ¡Pero oye! Habéis preferido la demostración con series.
Con esto hemos demostrado que la expresión general del filtro EMA es en realidad una media ponderada cuyos factores de ponderación siguen una progresión exponencial de parámetro beta, y que es necesario que beta sea mayor o igual a 0 y menor que 1 para que el sistema sea estable.
Filtro paso bajo y paso alto en Arduino
Aquí tenemos una implementación sencilla de un filtro de paso bajo y paso alto exponencial (EMA). En el ejemplo vamos a filtrar una serie de integer desordenados que simulan una señal como la que podríamos obtener al realizar una medición. Accedemos a estos valores a través de la función GetMeasure(), que simula el proceso de adquisición de datos.
Los resultados se muestran por puerto serie. Si empleáis el Serial Plotter del IDE Standard podréis ver los resultados gráficamente de forma sencilla.
float EMA_ALPHA = 0.6;
int EMA_LP = 0;
int EMA_HP = 0;
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
void setup()
{
Serial.begin(115200);
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
int filteredLP = EMALowPassFilter(value);
int filteredHP = EMAHighPassFilter(value);
Serial.print(value);
Serial.print(",");
Serial.print(filteredLP);
Serial.print(",");
Serial.println(filteredHP);
}
}
void loop()
{
delay(10000);
}
int EMALowPassFilter(int value)
{
EMA_LP = EMA_ALPHA * value + (1 - EMA_ALPHA) * EMA_LP;
return EMA_LP;
}
int EMAHighPassFilter(int value)
{
EMA_LP = EMA_ALPHA * value + (1 - EMA_ALPHA) * EMA_LP;
EMA_HP = value - EMA_LP;
return EMA_HP;
}Los resultados en el Serial Plotter del IDE Estándar serán los siguientes,
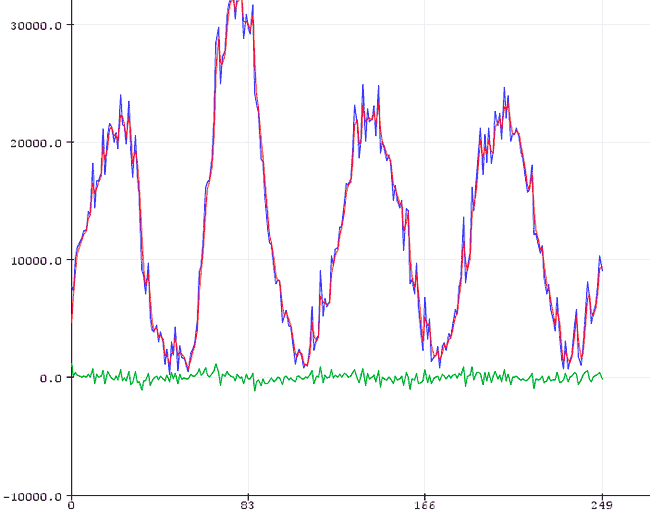
Filtro de paso bajo y alto en una librería
¿Y si lo metemos en una librería para que sea más cómodo de usar? Por supuesto que sí, aquí una librería Single EMA Filter para Arduino. ¡A disfrutarlo!
Descarga el código
Todo el código de esta entrada está disponible para su descarga en Github.