Continuamos con las entradas destinadas a convertirnos unos expertos 3D dentro de la sección de impresión 3D. En la entrada anterior vimos los distintos tipos de representaciones de objetos 3D. En esta entrada veremos los procesos de conversión entre ellos.
Al igual que la entrada anterior, avisamos que si lo que buscáis es imprimir lo antes posible esta entrada quizás os aporte poco o casi nada. Pero ya habíamos quedado en que vosotros no buscáis imprimir sin más, si no convertiros en unos auténticos “masters” del 3D que sacan el máximo a su impresora 3D.
Entender las conversiones es especialmente importante en la impresión 3D (y aún más en escaneado 3D) porque, como vimos en la visión general del proceso de impresión 3D, vamos a trabajar con sólidos (ficheros CAD) y mallas (ficheros STL).

Esto es incluso más cierto a medida que la tendencia de los programas 3D, como Fusion360, que permitir trabajar simultáneamente con sólidos, superficies, y mallas.
Así evitaremos oír “puedes decirme el diámetro de esa pieza escaneada en 3D”, sorprendernos de que no podemos editar un fichero STL con nuestro software CAD (fácilmente) o de que nuestro agujero perfectamente redondo es un polígono con lados rectos cuando lo imprimimos en 3D.
Pero antes de empezar a ver los procesos de transformación, vamos a poner un poco todo en perspectiva viendo un poquito (poquito, lo prometo) de teoría.
Visión general
En resumen, tenemos dos formas de representar geometría en un ordenador, representaciones continuas y discretas. La forma continua emplea ecuaciones y modelos matemáticos, mientras que la forma discretizada contiene información únicamente en ciertos puntos del espacio.
En realidad, estos dos modos continuo y discreto, nos acompañan en muchas más situaciones que representar geometría.
Clasificando las formas de representar objetos 3D que vimos en la entrada anterior, en resumen, tenemos:
Discretos: Nubes de puntos y mallas (incluyen trianguladas, quads, y subdivisión).
Continuas: Superficies y sólidos.

En principio, pasar de un modelo continuo a un modelo discreto es relativamente sencillo aplicando alguno de los varios algoritmos posibles. Este proceso de muestreo básicamente tomará los valore del modelo continuo en ciertos puntos, desechando el resto de la información.
Cuando más estrecho sea intervalo de muestreo más cercano será el modelo discreto al continuo. Pero, a cambio, tendremos un mayor número de puntos, lo que significará un mayor tamaño de archivo y mayor carga de procesado.
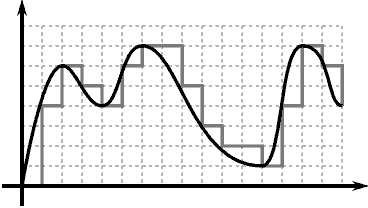
Por el contrario, el paso de un modelo discreto a uno continuo no es trivial, siendo un ejercicio de interpolación. Estamos intentando “ajustar” un modelo matemático a un modelo discreto, en el que hemos perdido datos en el muestreo.
Si alguna vez habéis ajustado una curva a una serie de puntos sabréis que, en general, no es sencillo y normalmente implica la minimización de “algún tipo de error”. Pero si intentamos reducir demasiado llegamos a una solución “continua” idéntica a la discreta.
Analogía en 2D
Seguramente se entiende mejor todo lo anterior si ponemos un ejemplo en 2D. Como sabemos, tenemos dos formas de trabajar con gráficos e imágenes en 2D.
Por un lado tenemos formatos vectoriales que creamos con programas de diseño (AutoCAD, Illustrator, etc), en el que las entidades son tratadas como objetos matemáticos continuos (líneas, círculos, splines, etc).
Por otro lado tenemos el formato bitmap (o raster), que guarda la información en una cuadrícula discreta en la cual cada punto tiene un color (RGB, CMYK, trasparencia, etc).
Pasar de un formato vectorial a uno raster es siempre posible mediante alguno de los algoritmos disponibles. Básicamente preguntamos en cada punto de la rejilla que color le tocaría según el modelo vectorial.
La diferencia entre algoritmos es el criterio para determinar el color de cada pixel, y sus vecinos, en función de la distancia al modelo, lo que da lugar a modelos más o menos suavizados o enfocados.
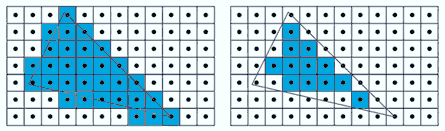
Pero siempre es posible convertir en una imagen que “de lejos” parece el objeto original. Si hacemos zoom, veremos los pixels. Es decir, es un proceso con pérdidas. Si queremos mayor detalle deberemos aumentar la resolución (es decir, reducir el intervalo de muestreo), lo que implicará un mayor tamaño del archivo.
Sin embargo, también sabréis que el proceso contrario, vectorizar una imagen ráster no es tan sencillo. Existen programas que incorporan un procesos automáticos pero, en general, el resultado no suele ser bueno y requieren intervención del usuario.

De hecho, si intentamos vectorizar una imagen capturada, por ejemplo, con una cámara, la vectorización tendrá que realizar una segmentación de colores (“agrupar” zonas de colores similares) o acabaremos con una imagen vectorial que es un rectángulo para cada pixel.
Creo que ilustra bastante bien lo comentado anteriormente sobre modelos continuos, discretos, muestro e interpolación. Pues prepararos porque en 3D es lo mismo (de hecho, es incluso peor).
Procesos de conversión entre representaciones 3D
Vamos a ver los distintos procesos de conversión, agrupando por el modelo (discreto o continuo) del origen y el destino.
Discreto a Discreto
Empezamos con la opción más sencilla y seguramente menos interesante. Convertir de una malla a un objeto de puntos es sencillo. Simplemente hay que crear un punto en cada uno de los vértices de la malla. Y, salvo casos muy extraños, no nos va a ser de utilidad.
El caso opuesto si es mucho más frecuente e interesante. Lo tenemos cada vez que tenemos que obtener un modelo 3D a partir de un escaneado 3D (que recordemos siempre devuelven una nube de puntos).
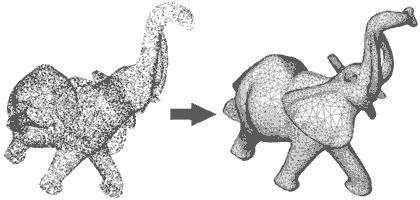
Es un proceso con complejidad matemática alta y muchos estudios realizados al respecto (se sigue estudiando hoy en día). Existen varios algoritmos para realizar este proceso, como el conocido Delaunoy, o el más empleado el Pivot-Ball junto con variantes.
Pero, en general, podemos decir que es un proceso que actualmente está bastante bien resuelto e implementado en muchos softwares 3D.
Convertir mallas a mallas es un proceso mucho más habitual de lo que podría parecer. ¿Para qué que queremos convertir una malla en otra? Pues para tener una malla más conveniente, según algún criterio. Este proceso en general se denomina retopología.
Ejemplos son convertir una malla en una con un mayor número de puntos, lo que incluye la subdivisión o el teselado, a costa de tener un fichero de mayor tamaño.
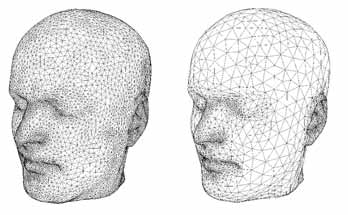
También tenemos el proceso contrario, simplificar malla, que reduce la cantidad de puntos intentando preservar el detalle. En general, se emplean algoritmos que intentan sustituir polígonos o eliminarlos en las zonas de menor curvatura.
Pero también hay otros procesos como suavizado, erosión, relajación, “enfocado” (aumentar detalles). Por último, en el ámbito de los videojuegos, films, etc, la retopología frecuentemente busca obtener una malla más apropiada para animar, o texturizar.
Continuo a continuo
Ya vimos que, básicamente, un sólido está formado por superficies a las que se les ha añadido el concepto de “dentro y fuera”. Por tanto, la conversión de sólidos a superficies es prácticamente inmediato. A este proceso se le puede denominar “descomponer” o “explotado”, depende del software 3D.
El caso contrario no es tan sencillo, porque no todas las superficies generan un sólido. En general, si tenemos una superficie cerrada y sin puntos singulares (bucles cerrados sobre sí mismos, y otras anomalías) el proceso es posible.
Si en lugar de una única superficie tenemos varias, deberemos juntarlas y tratarlas con las herramientas de superficies disponibles hasta tener un modelo válido para convertir en sólido.
No existe un nombre estándar para esta conversión, pero a veces veremos referida la operación como “solidificar” o simplemente “convertir a sólido”en los softwares 3D.
Continuo a discreto
Entramos en los procesos más interesantes. La conversión de superficies/sólidos es un proceso muy frecuente y normal, más de lo que podría parecer. Tu ordenador lo hace siempre que muestra un modelo CAD en tu pantalla, ya que la GPU está diseñada para trabajar con mallas.
En nuestro caso, nuestra impresora 3D no es capaz de trabajar con sólidos o superficies (quizás te sorprenda, pero la mayoría de procesos de fabricación industrial tampoco). Así que para imprimir nuestros ficheros CAD tenemos que convertirlos en ficheros triangulados (normalmente a STL).
Afortunadamente, como ya adelantábamos, en general este proceso de triangulación es relativamente sencillo. Existen diferentes algoritmos (uniforme, espacial, de curvatura) para obtener una malla a partir de un sólido o superficie.
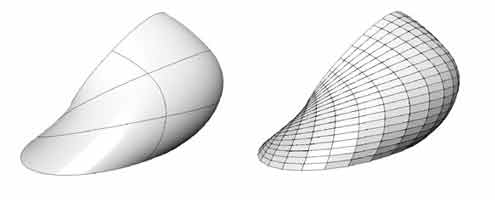
Como todo proceso de muestreo la triangulación es un proceso con pérdidas. Estamos representando objetos, con curvas con (teóricamente) un detalle infinito por una serie de triángulos con lados rectos. Si los triángulos son suficientemente pequeños no notaremos la diferencia, a una determinada distancia.
Si queremos aumentar la calidad, tendremos que reducir el tamaño de los triángulos. La mayoría de softwares CAD permiten configurar el grado de detalle al exportar a mallas. Pero, como hemos avanzado, esto implica mayor tamaño de archivo y tiempo de proceso. Como de costumbre, lo importante es llegar a un compromiso en precisión y calidad.

Discreto a continuo
Llegamos al caso más difícil, convertir una superficie mallada a una superficie/sólidos. Este proceso se denomina ingeniería inversa y, en general, no es un proceso sencillo y requiere intervención de una persona para obtener buenos resultados.

Hay que tener en cuenta que una malla triangulada, y sobre todo en aquellas que provienen de captación/escaneado de la realidad, las curvas son aproximaciones poligonales. Pero es mucho peor aún, los planos no tampoco son planos. Necesitamos interpolar y ajustar superficies a los puntos.
Existen programas dedicados que proporcionan asistencia en el proceso, y la mayoría de software CAD empiezan a incorporar funciones para trabajar con modelos mallados, y proporcionando herramientas que ayudan a realizar este proceso.
También existen procesos “automáticos” que convierten la malla en una serie de superficies que aproximan el objeto original. Puede ser suficiente para trabajar con ellos en software de CAD, pero no es (ni mucho menos) un sólido perfecto como el que tendríamos si lo hubiéramos dibujado.
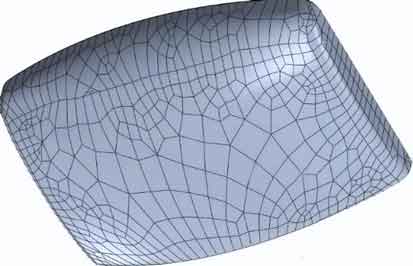
Por otro lado, aún en el caso de que usemos las herramientas para ajustar superficies (planos, cilíndricas, cónicas) de las herramientas de ingeniería inversa, en la mayoría de casos el resultado sigue sin ser perfecto. El radio que (por lógica) en el diseño original era 50mm, ajustado y medido es 50.13mm. Dos cilindros que eran concéntricos ya no lo son. Lo mismo con paralelismos, perpendiculares, simetrías, patrones, etc.
En principio el proceso de ingeniería completo requiere “casi” redibujar la pieza por completo tomando el modelo como base. A veces lleva incluso más tiempo que dibujarla desde cero, porque cuando la dibujas de cero lo haces “como quieres” y en la ingeniería inversa tienes que ajustarte a un modelo.

Hasta aquí este par de entradas destinadas a introducir la base de la representación de objetos 3D y sus procesos de conversión, como previo a meternos de lleno en el mundillo del diseño e impresión 3D.
En las próximas entradas de la sección nos adentraremos en el diseño 3D presentando los diferentes tipos de software de diseño 3D y los principales softwares de diseño CAD. ¡Hasta pronto!
