In the previous post we extensively covered the EMA exponential filter applied to low-pass and high-pass filtering. In this post we will delve deeper into the topic and extend it to bandpass and bandstop filters.
To recap, let’s remember that a signal can be considered as a sum of frequency components. An ideal low-pass filter (which is impossible to obtain in the real world) would let the components below a cutoff frequency (Fc) pass. On the other hand, an ideal high-pass filter would let the components above a cutoff frequency pass.
Bandpass and bandstop filters require two cutoff frequencies that, in a generic way, we will call the lower cutoff frequency (Fci) and the upper cutoff frequency (Fcs).
An ideal bandpass filter only lets the frequencies higher than the lower cutoff pass and lower than the upper cutoff pass, that is, the frequency components in a band between both cutoff frequencies (Fci to Fcs).
Filters have a wide range of applications in electronics. You use them every day when you use a device that “tunes in” to a signal. This includes all forms of communication, from radio, television, mobile, WiFi, among almost an infinite number of applications.
On the other hand, the bandstop filter is the opposite case, that is, it eliminates the components between both cutoff frequencies, so it only lets the frequencies from -∞ to Fci and from Fcs to +∞ pass.
While they are not as frequent, they still have a huge range of applications when we want to eliminate a signal of known frequency. For example, we can eliminate AC frequencies, filter the vibrations of a machine rotating at known revolutions, or eliminate flickering in optical sensors and cameras caused by artificial lights powered by AC.
Generate a bandpass and bandstop filter
To generate a bandpass or bandstop filter we generally start with a low-pass filter and obtain the rest through operations with the original signal. The results would be analogous starting from a high-pass filter, but the algorithms to directly generate a high-pass filter are much less frequent than those for low-pass filters.
Let’s remember that if we had our imaginary (and by this point almost famous) ideal low-pass filter, generating a high-pass filter would be as simple as subtracting the low-pass filter from the original signal.
To visualize it, let’s imagine the spectrum of the signal with its frequency components from -∞ to +∞. The low-pass filter only lets the frequencies below the cutoff frequency (Fc) pass, that is, the frequencies from -∞ to Fc.
Therefore, subtracting the low-pass filter’s result from the spectrum lets the frequencies from Fc to +∞ pass, which corresponds precisely to the behavior of a high-pass filter.
By extension, to generate a bandpass filter we only have to subtract the low-pass filter of the higher frequency from the low-pass filter of the lower frequency.
The upper low-pass filter lets the frequencies from -∞ to Fcs pass, and the lower low-pass filter lets the frequencies from -∞ to Fci pass, so subtracting both values lets the frequencies from Fci to Fcs pass, which is exactly what we want.
Finally, to obtain the bandstop filter we only have to subtract the bandpass filter from the original signal, which lets the frequencies from -∞ to Fci and Fcs to +∞ pass.
At this point, it is worth remembering that most of what is explained here is applicable to a wide variety of filters. In this post, we use the EMA exponential filter because it is widely used and yields good results with a simple implementation and high computational efficiency.
However, any algorithm that “smooths out” a signal can be used as a low-pass filter (with better or worse characteristics) and, therefore, is susceptible to giving rise to a high-pass, bandpass, and bandstop filter.
Bandpass filter results
As we said in the previous post, in the exponential filter the amount of smoothing is controlled through the alpha factor. It is not easy to find a simple relationship with the cutoff frequency, among other things, because the sampling frequency is unknown and variable.
What we do know is that the smaller the alpha factor, the greater the smoothing of the signal, and therefore, the lower the cutoff frequency. Remember that, as a negative point, the delay between the filtered signal and the original signal will also be greater.
In a bandpass and bandstop filter, we will have two alpha factors that we will call Low and High which correspond, respectively, to the lower and upper cutoff frequency.
Next, we will see the effect of these factors with the results of the bandpass filter for different combinations of alpha Low and High applied to the same signal.
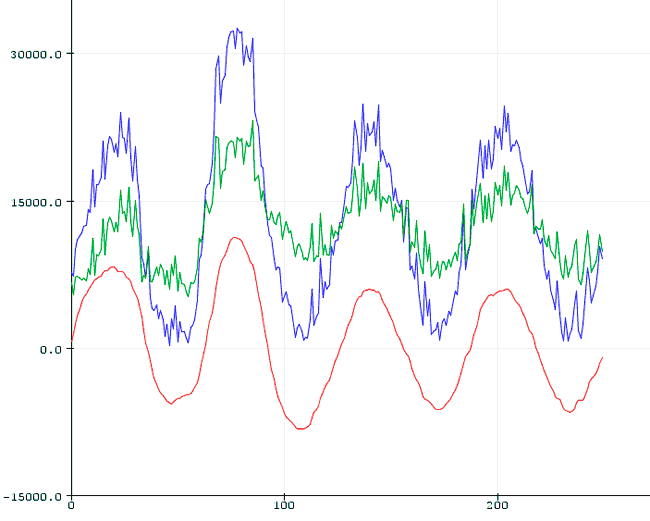
These are the results for a Low alpha of 0.025 and High alpha of 0.5. Note that the lower filter has eliminated the bias after a few oscillations, while the upper filter has smoothed out some of the high-frequency noise.
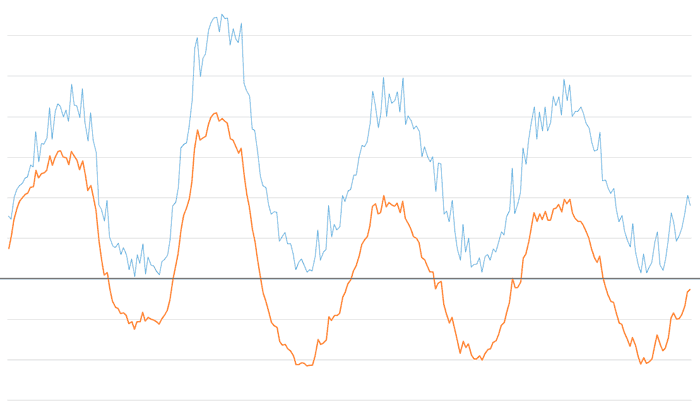
If we decrease the high alpha factor to 0.3, maintaining the low at 0.025, we see that most of the high-frequency noise is eliminated.
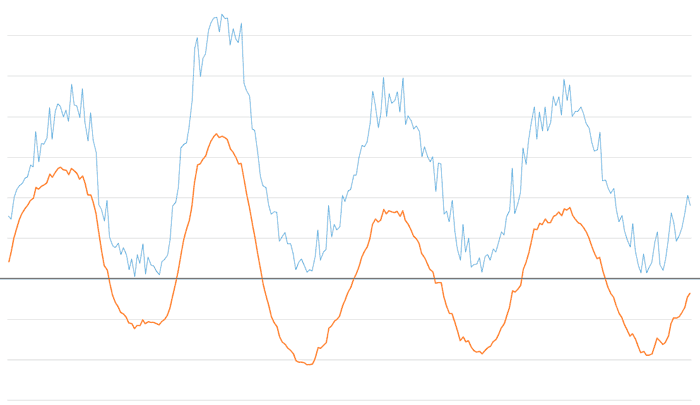
And if we decrease the high alpha factor even further to 0.15, we will see that we have eliminated all components except the fundamental harmonics of the example signal.
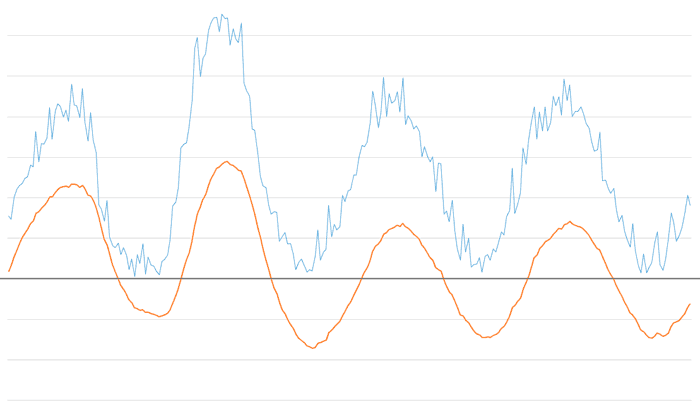
In other words, in a single filter, we have eliminated high-frequency noise and the signal bias. Not bad for such a simple filter, right?
Bandpass and bandstop filter on Arduino
Here is a simple implementation of an exponential bandpass and bandstop filter (EMA). In the example, we will filter a series of disordered integers that simulate a signal as we could obtain when making a measurement. We access these values through the GetMeasure() function, which simulates the data acquisition process.
The results are shown through the serial port. If you use the Serial Plotter of the Standard IDE, you can easily see the results graphically.
float EMA_ALPHA_LOW = 0.025;
float EMA_ALPHA_HIGH = 0.1;
int EMA_LP_LOW = 0;
int EMA_LP_HIGH = 0;
int EMA_BP = 0;
int EMA_BS = 0;
int values[] = {7729, 7330, 10075, ... };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index-1];
}
void setup()
{
Serial.begin(115200);
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
int filteredBP = EMABandPassFilter(value);
int filteredBS = EMABandStopFilter(value);
Serial.print(value);
Serial.print(",");
Serial.print(filteredBP);
Serial.print(",");
Serial.println(filteredBS);
}
}
void loop()
{
delay(10000);
}
int EMABandPassFilter(int value)
{
EMA_LP_LOW = EMA_ALPHA_LOW * value + (1 - EMA_ALPHA_LOW) * EMA_LP_LOW;
EMA_LP_HIGH = EMA_ALPHA_HIGH * value + (1 - EMA_ALPHA_HIGH) * EMA_LP_HIGH;
EMA_BP = EMA_LP_HIGH - EMA_LP_LOW;
return EMA_BP;
}
int EMABandStopFilter(int value)
{
EMA_LP_LOW = EMA_ALPHA_LOW * value + (1 - EMA_ALPHA_LOW) * EMA_LP_LOW;
EMA_LP_HIGH = EMA_ALPHA_HIGH * value + (1 - EMA_ALPHA_HIGH) * EMA_LP_HIGH;
EMA_BP = EMA_LP_HIGH - EMA_LP_LOW;
EMA_BS = value - EMA_BP;
return EMA_BS;
}The results in the Serial Plotter of the Standard IDE will be as follows,
Bandpass and bandstop filter in a library
And what if we put it in a library to make it more convenient to use? Of course, here is a Double EMA Filter library for Arduino. Enjoy!
Download the code
All the code from this post is available for download on Github.