We continue with digital filters as a way to improve the values obtained from sensor measurements in our electronics and robotics projects with Arduino.
So far we have seen the moving average filter and the EMA exponential filter for low-pass and high-pass filtering and double EMA for band-pass and stop-band filtering. These filters are simple and efficient to implement but have the disadvantage of being less robust/stable in the presence of outliers (points that deviate significantly from the real value).
This is because both filters (moving average and exponential filter) are based on the mean as a trend estimator. As we saw when discussing fast median calculation on Arduino, the mean is a non-robust trend estimator. Its popularity is largely due to the simplicity of calculation and because it is a function we can manipulate and derive.
The best example to illustrate the instability of the mean is its behavior with outliers. A single anomalous point can cause a large deviation in the mean, ruining an entire series of measurements, which shows the lack of robustness of the mean as a trend estimator.
Fortunately, the mean is not the only trend estimator. Here statistics comes to the rescue, specifically the branch of robust statistics, which is responsible for performing calculations with greater stability than traditional statistics. And precisely robust statistics uses the median as an indicator of trend.
In this post, we will focus on efficiently implementing a moving median filter, lightweight enough to fit on a microprocessor like Arduino.
The Moving Median Filter
Similar to the moving average filter, the moving median filter defines a window of N elements, which collects the last N measurements. The filter value is the median of the values contained in the window.
Increasing the window size increases the smoothing of the signal but adds a delay to the signal (as happened with the moving average and EMA filters) because it is necessary to “wait” for more points to be sampled.
The window size will depend on the characteristics of our system and the signal to be filtered, but sizes from 5 to 11 are common. In general, odd window sizes are preferred to avoid having to average between two samples, which would eliminate part of the median’s filtering capability.
A moving median filter is a very useful and widely used tool in electronics. They are widely used in data acquisition systems and sensor capture for noise removal, for example, in gyroscopes and accelerometers.
The moving median filter presents better characteristics for filtering certain types of signals, especially those with outliers or salt and pepper noise (noise that causes points to go to the minimum or maximum possible).
On the other hand, using the median as a filter also has its disadvantages. The most obvious is that, in general, computationally it is a more expensive calculation. It is commonly considered that calculating the median involves sorting all the contained values, which we demonstrated is not true when discussing median calculation.
Furthermore, the median filter can only return sampled points, so we lose the “interpolation” (subsampling) capability we can get with other filters. This causes filtered signals to be “angular” and present discrete jumps.
However, it is possible to improve the behavior by combining the moving median filter with an EMA exponential filter, keeping in mind that the factor of both filters will accumulate. Therefore, we must reach a compromise, reducing the window size and the EMA alpha to not skyrocket the overall delay.
Results of the Median Filter
To illustrate the behavior of the moving median filter, we will show the results for the same simulated input signal and different window sizes.
The first figure shows the median filter for a window size of 3. We see that it has removed most of the signal’s “peaks”, which corresponds to what we mentioned about the median filter’s capability for outlier and noise removal.
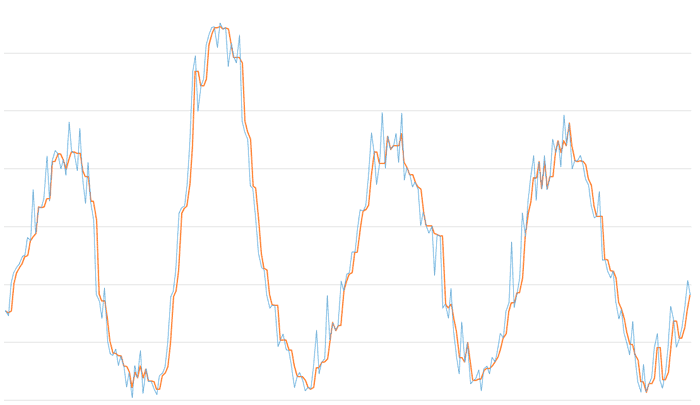
However, a window size of 3 is usually insufficient because if two anomalous points coincide, the filter would only be able to absorb/eliminate one.
The following graph shows the result for a window size of 5. With a larger window, the median filter increases its robustness against noise. However, we observe the angular and “jumpy” behavior we mentioned before.
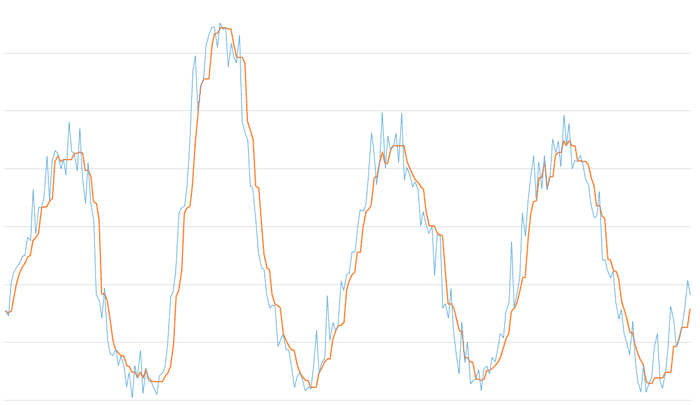
The next graph shows the result for a window size of 11. The filtered signal increases its smoothness, but the delay starts to become evident.
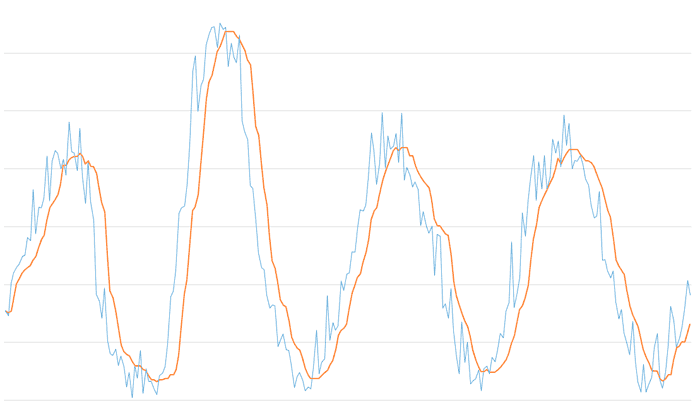
Finally, the last graph shows the combination of a median filter with a window size of 3 with an EMA exponential filter of Alpha 0.3.
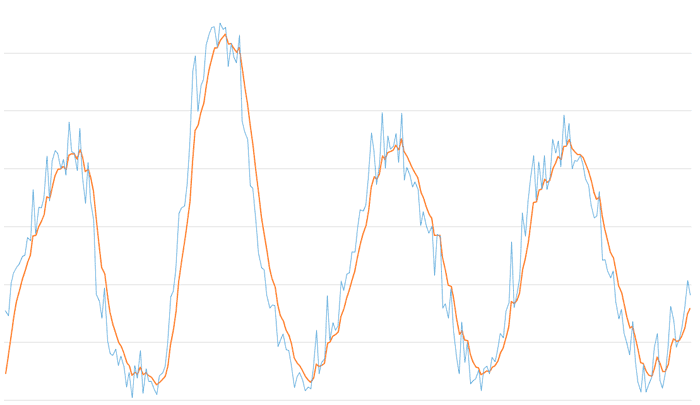
We see that the combination of a median filter with a reduced window (5 would be a good value) along with a moderate alpha EMA provides the noise and outlier filtering of the median along with the smoothness and subsampling provided by the EMA, while keeping the delay at acceptable levels.
Implementing a Median Filter on Arduino
We are going to test three different implementations for a moving median filter. I’ll give you a spoiler: the most efficient one will, logically, be the last one. But we will present all three, especially for those stubbornly implementing the median filter with a simple sorting algorithm :).
Median Filter with Quick Sort
The first option is to sort the window values with a sorting algorithm. In the post about sorting with QuickSort we already demonstrated that it is much faster than other alternatives like the famous (and inefficient) bubble sort or the slightly less famous (and not much less inefficient) insertion sort.
Therefore, we will only test our Quick Sort algorithm. A lightweight implementation of the median filter with Quick Sort would be the following.
const int windowSize = 3;
int buffer[windowSize];
int medianBuffer[windowSize];
int* medianBufferAccessor = medianBuffer;
#define MEDIAN(a, n) a[(((n)&1)?((n)/2):(((n)/2)-1))];
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*medianBufferAccessor = value;
medianBufferAccessor++;
if (medianBufferAccessor >= medianBuffer + windowSize)
medianBufferAccessor = medianBuffer;
}
int elementCount;
float AddValue(int value)
{
appendToBuffer(value);
if (elementCount < windowSize)
++elementCount;
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
AddValue(value);
memcpy(buffer, medianBuffer, sizeof(medianBuffer));
QuickSortAsc(buffer, 0, elementCount - 1);
int med = MEDIAN(medianBuffer, windowSize);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(value);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
void QuickSortAsc(int* arr, const int left, const int right)
{
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
while (i <= j)
{
while (arr[i]<pivot) i++;
while (arr[j]>pivot) j--;
if (i <= j)
{
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
if (left<j)
QuickSortAsc(arr, left, j);
if (i<right)
QuickSortAsc(arr, i, right);
}
Median Filter with Quick Median
The next evolution is that, as we saw in the post about fast median calculation on Arduino, there are more efficient algorithms to calculate the median that do not require full sorting of the vector.
In that post, we tested different algorithms, finally opting for the Quick Select algorithm modified by Wirth for its high efficiency and relatively simple implementation, suitable for a processor like Arduino.
Therefore, we are going to test implementing the median filter using the Wirth Quick Select algorithm to calculate the window median. A disadvantage of this method is that the Quick Select algorithm modifies the vector, so we will have to copy the window into an intermediate buffer for the calculation.
The implementation would be as follows.
const int windowSize = 33;
int buffer[windowSize];
int medianBuffer[windowSize];
int* medianBufferAccessor = medianBuffer;
#define ELEM_SWAP(a,b) { int t=(a);(a)=(b);(b)=t; }
#define MEDIAN(a,n) kth_smallest(a,n,(((n)&1)?((n)/2):(((n)/2)-1)))
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*medianBufferAccessor = value;
medianBufferAccessor++;
if (medianBufferAccessor >= medianBuffer + windowSize)
medianBufferAccessor = medianBuffer;
}
int elementCount;
float AddValue(int value)
{
appendToBuffer(value);
if (elementCount < windowSize)
++elementCount;
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
AddValue(value);
memcpy(buffer, medianBuffer, sizeof(medianBuffer));
int med = MEDIAN(medianBuffer, elementCount);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(value);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
int kth_smallest(int a[], int n, int k)
{
int i, j, l, m;
int x;
l = 0;
m = n - 1;
while (l<m)
{
x = a[k];
i = l;
j = m;
do {
while (a[i]<x) i++;
while (x<a[j]) j--;
if (i <= j)
{
ELEM_SWAP(a[i], a[j]);
i++;
j--;
}
} while (i <= j);
if (j<k) l = i;
if (k<i) m = j;
}
return a[k];
}
Quick Median Filter Median Filter
The last algorithm tested is the algorithm proposed by Phil Ekstrom in November 2000. Ekstrom uses a combination of circular buffer and linked list to improve the efficiency of the median filter, especially for large window sizes.
Similar to the motivation for using a circular buffer to calculate the moving average filter, Ekstrom’s algorithm finds its origin in the fact that adding a new value and removing the oldest one from the window does not substantially modify its structure. In particular, it is not necessary to process it completely.
Ekstrom uses a circular buffer to store the window elements according to their age. On the other hand, each element contains a pointer to the next smaller element, forming a linked list.
Adding a new element to the circular buffer and inserting an element in the linked list is immediate. The only real computational cost is finding the insertion point, for which it is necessary to traverse the linked list.
The implementation is simple and suitable for a microprocessor like Arduino. However, it is possible to improve its efficiency, just as there are algorithms with better efficiency, at the cost of greater memory usage.
#define MEDIAN_FILTER_WINDOW 7
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
int med = medianFilter(value);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(values[iCount]);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
#define STOPPER 0
uint16_t medianFilter(uint16_t value)
{
struct node
{
struct node *next;
uint16_t value;
};
static struct node buffer[MEDIAN_FILTER_WINDOW] = { 0 };
static struct node *iterator = buffer;
static struct node smaller = { nullptr, STOPPER };
static struct node bigger = { &smaller, 0 };
struct node *successor;
struct node *accessor;
struct node *accessorPrev;
struct node *median;
uint16_t i;
if (value == STOPPER)
value++;
if ((++iterator - buffer) >= MEDIAN_FILTER_WINDOW)
iterator = buffer;
iterator->value = value;
successor = iterator->next;
median = &bigger;
accessorPrev = nullptr;
accessor = &bigger;
if (accessor->next == iterator)
accessor->next = successor;
accessorPrev = accessor;
accessor = accessor->next;
for (i = 0; i < MEDIAN_FILTER_WINDOW; ++i)
{
if (accessor->next == iterator)
accessor->next = successor;
if (accessor->value < value)
{
iterator->next = accessorPrev->next;
accessorPrev->next = iterator;
value = STOPPER;
};
median = median->next;
if (accessor == &smaller)
break;
accessorPrev = accessor;
accessor = accessor->next;
if (accessor->next == iterator)
accessor->next = successor;
if (accessor->value < value)
{
iterator->next = accessorPrev->next;
accessorPrev->next = iterator;
value = STOPPER;
}
if (accessor == &smaller)
break;
accessorPrev = accessor;
accessor = accessor->next;
}
return median->value;
}
Bonus: 3-size median filter
If we are using a window size 3, the filter allows for a much simpler and more efficient implementation.
const int windowSize = 3;
int medianBuffer[windowSize];
int* medianBufferAccessor = medianBuffer;
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*medianBufferAccessor = value;
medianBufferAccessor++;
if (medianBufferAccessor >= medianBuffer + windowSize)
medianBufferAccessor = medianBuffer;
}
float AddValue(int value)
{
appendToBuffer(value);
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
AddValue(value);
int med = median3(medianBuffer);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(value);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
int median3(int arr[])
{
if ((arr[0] <= arr[1]) && (arr[0] <= arr[2]))
return (arr[1] <= arr[2]) ? arr[1] : arr[2];
else if ((arr[1] <= arr[0]) && (arr[1] <= arr[2]))
return (arr[0] <= arr[2]) ? arr[0] : arr[2];
else
return (arr[0] <= arr[1]) ? arr[0] : arr[1];
}
Comparison
Here is the time required to execute the different algorithms, for different window sizes. All of them have been performed on an Arduino Nano 16Mhz. The results are shown in us.
| Window | QuickSort | Wirth | Ekstrom | Direct |
|---|---|---|---|---|
| 3 | 23.28 | 23.02 | 14.14 | 5.29 |
| 5 | 44.03 | 32.67 | 18.02 | - |
| 7 | 64.83 | 42.37 | 22.37 | - |
| 9 | 94.34 | 53.15 | 26.83 | - |
| 11 | 115.94 | 64.86 | 30.83 | - |
| 33 | 403.73 | 189.25 | 80.78 | - |
As we can see, the Ekstrom algorithm is much faster than the rest of the alternatives, even having used very fast algorithms for sorting (Quick Sort) and calculating the median (Quick Select Wirth).
Logically, for a window size of 3, the direct algorithm is much faster, but we normally won’t use a size of 3 because, as we have mentioned, it is too small.
For common values of (from 5 to 11) the median filter with the Ekstrom algorithm is about 2 times faster than the median calculation with Quick Select, and 3 times faster than sorting with Quick Select. Larger window sizes provide even greater advantages in favor of Ekstrom.
Fast median filter in a library
What if we clean up and improve the code, and put it into a library to make it more convenient to use? Of course, yes, here is a Median Filter library for Arduino. Enjoy it!
Download the code
All the code in this post is available for download on Github.