In the entry on multiple sampling in Arduino, we already introduced that reducing noise in measurements will be a constant (and almost an obsession) in any of our electronics and robotics projects. We also saw that the solution involves taking multiple measurements and using an algorithm to combine the measurements.
Let’s start with the application of filters themselves, understanding a digital filter as an algorithm that allows us to combine several points of a sampled signal to obtain a value with more significance than the individual points.
There are many possible digital filters. In this post, we are going to see the moving average filter, a widely used digital filter because it is intuitive, easy to implement, and quick to calculate.
In the moving average filter, we take the last N received values (which we will call the “window”) and calculate their average. The result is a smoothed signal that eliminates some of the high-frequency noise. The size of the window has a great influence on the behavior of the filter, as we will see later.
The moving average filter is very easy to implement since the calculation of the average only requires adding the N elements of the window and dividing by N.
The algorithm’s efficiency improves substantially by using a circular buffer. The motivation is that adding a new element to the window “affects” the sum very little. It is only necessary to subtract the first value from the window and add the new value.
By using a circular buffer, we can calculate the new filtered value without needing to go through the N elements of the window, which improves the efficiency of the algorithm from O(n) to O(1) with respect to the window size.
Despite the advantages of the moving average filter, especially in terms of efficiency and simplicity, it also has its disadvantages, mainly related to the weakness of using the average as an estimator of trend.
In particular, the moving average filter is unstable in the presence of spurious points (anomalous points far from the real value). In these cases, it is more convenient to use a median filter, or a combination of both.
Influence of the window size
The window size conditions the behavior of the filter. A value of 1 would leave the signal unchanged. The larger the size, the more the signal is smoothed.
However, increasing the window size also has negative consequences. On the one hand, we can eliminate components of the signal in which we are interested (authentic variations of the signal and not just noise). On the other hand, it introduces a phase shift between the original signal and the filtered signal, since we need to accumulate N elements before providing a value.
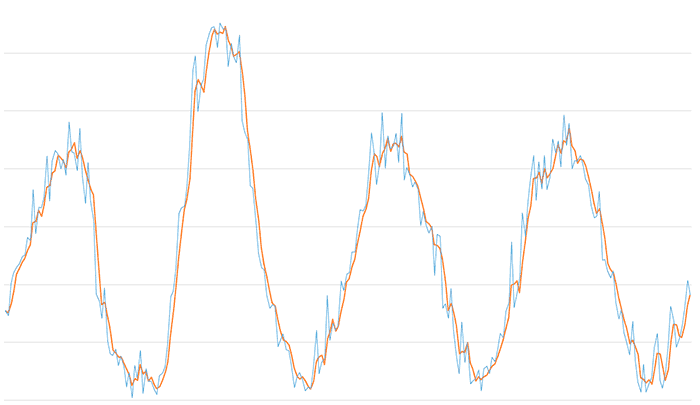
Here are the results of a filter for the same signal with a window size of 3,
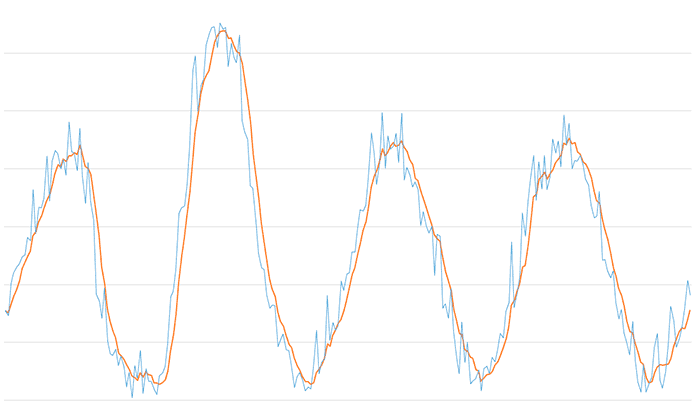
For a window size of 5,
And for a window size of 10,
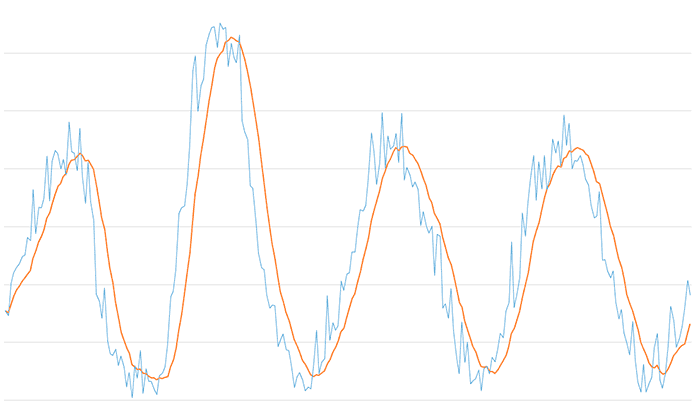
The appropriate value for the window size depends entirely on the type of signal we have (amount of noise, frequency, etc.) and our system (sampling frequency, reliability, etc.). However, values between 3 and 10 are common.
Implementation in Arduino
Here we have a lightweight implementation of a moving average filter using a circular buffer to store the N values of the window.
In the example, we are going to filter a series of disordered integers that simulate a signal as we could obtain when taking a measurement. We access these values through the GetMeasure() function, which simulates the data acquisition process.
const int windowSize = 5;
int circularBuffer[windowSize];
int* circularBufferAccessor = circularBuffer;
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
static int index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*circularBufferAccessor = value;
circularBufferAccessor++;
if (circularBufferAccessor >= circularBuffer + windowSize)
circularBufferAccessor = circularBuffer;
}
long sum;
int elementCount;
float mean;
float AddValue(int value)
{
sum -= *circularBufferAccessor;
sum += value;
appendToBuffer(value);
if (elementCount < windowSize)
++elementCount;
return (float) sum / elementCount;
}
void setup()
{
Serial.begin(115200);
for (int iCount = 0; iCount < valuesLength; iCount++)
{
float med = AddValue(getMeasure());
Serial.print(values[iCount]);
Serial.print(",\t");
Serial.println(med);
}
}
void loop()
{
}If we run the code, we will see the following result of the original value and the filtered value.
If you use the Serial Plotter from the standard Arduino IDE, you can easily see the graph of the values.
Moving average filter in a library
What if we put it in a library to make it more comfortable to use? Of course, we can, here is a MeanFilter library for Arduino. Enjoy it!
Download the code
All the code from this post is available for download on Github.