Binary subtraction is another fundamental operation used to subtract one binary number from another.
As in decimal subtraction, the corresponding bits of the numbers are subtracted from right to left, taking into account borrows.
Binary subtraction can result in a negative outcome if the number being subtracted is greater than the number it is being subtracted from.
Try It
Borrow
The “borrow” occurs when a number cannot be subtracted from another due to its value. This happens when the number being subtracted is greater than the number it is being subtracted from.
In binary, this only happens when we try to subtract 1 from 0. In this case, the result is ‘1’, and a value is “borrowed” from the next most significant bit.
Example
For example, to subtract the binary number 1101 (13 in decimal) from 1011 (11 in decimal):
1011
- 1101
______
1110
The result is 1110, which equals -2 in decimal.
This is one of the most complex cases you will encounter, because the result was negative.
That is, the number we subtracted (13) was larger than the minuend (11).
Binary Subtraction with Two’s Complement
Binary subtraction is not difficult, but it can be a bit tedious. Generally, it is faster using the two’s complement method. This method allows converting subtraction into addition, and we know how to add two binary numbers “by hand” very quickly.
To subtract binary numbers using two’s complement, we follow these steps:
- Convert the number to be subtracted into its two’s complement.
- Add the number being subtracted from to the two’s complement.
- Discard any overflow bit at the end.
We could also do a manual procedure to subtract by hand very quickly, as we did with addition. But in general, it’s better to know two or three “tricks” to do things fast, than to try to learn 27 and then mix them all up or forget them all.
Example
Let’s subtract the binary number 1101 (11 in decimal) from the binary number 1011 (13 in decimal) using two’s complement:
1101
- 1011
_____
¿?¿?
First, we convert 1011 into its two’s complement. To do this, we invert all the bits and then add 1:
1011 (Original number) => Two's complement
0100 (Inverted bits)
+ 1 (Sum of 1)
_____
0101 (Two's complement of 1011)
- We add
1101with the two’s complement of1011:
1101 (Original number)
+ 0101 (Two's complement of 1011)
______
1 0010 (Result)
By discarding the overflow bit on the left, we get the final result: 0010, which equals 2 in decimal.
The advantages of using two’s complement for subtraction are that it simplifies the process for us and eliminates the need to handle borrows.
Bonus: How to Subtract 1 Quickly in Binary
Special bonus, how to quickly subtract 1 from a binary number. A very simple operation, but since it’s very common, it’s good to know how to do it.
Fortunately, subtracting 1 in binary is “a piece of cake”. Simply:
- Traverse the binary number from the right.
- Find the first
1you encounter and change it to0. - From that position to the right, everything becomes
1s.
For example, if we had to subtract 1 from 1000100000:
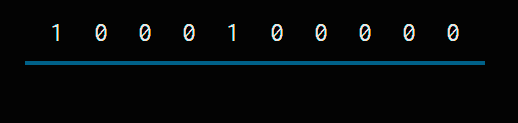
We look for the first 1:
We change it to 0 and, from there to the right, everything becomes 1.
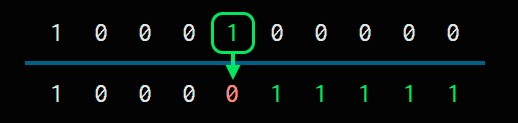
So the result is 1000011111. As you can see, subtracting one is very fast.
