How to add binary numbers

Addition is a fundamental arithmetic operation. Of course, in binary it’s no different, and adding binary numbers is one of the most frequent operations we will perform.

Fortunately, they are not very different from their decimal equivalents. In fact, in binary it’s even simpler. We simply add digit by digit from right to left, taking into account the carries.

It’s also important that, if we are working with fixed-size binary numbers, we consider overflow and underflow.

Try It

Binary Addition

Binary addition is a basic operation in the binary system. It is similar to addition in the decimal system, but it is performed with only two digits 0 and 1.

The summary of the process is as follows:

Carry

In addition, a “carry” occurs when the sum of two digits produces a result greater than or equal to the base, so it needs to be “carried” to the next position.

In binary this only happens when both bits we are adding are 1, in which case the sum is equal to ‘2.

In this case, the result is 0 and the carry means adding 1 to the next most significant bit.

  1011
+ 1101
______
 11000

  10101
+    11
______
 11000

How to Add Quickly in Binary

Adding in binary is quite simple. However, binary numbers are generally very long so it becomes… tedious.

Normally it’s not an operation you have to do by hand. But, if you ever have to do it, usually because your teacher feels like it, know that there are very fast ways to do the addition.

In fact, it’s very easy and fast to add binary numbers. Let’s start by analyzing what we will encounter. First, let’s assume we are not carrying.

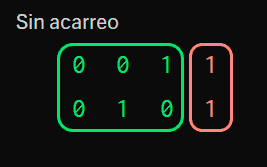
• If both are 0, the result is 0
• If one is 0 and the other 1 (or vice versa) they “mesh”, and make a 1
• The only difficult one is when we have 1 and 1, where we have a carry.

Now let’s see what happens when we are carrying.

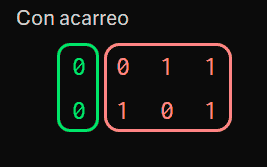
The interesting thing here is to see that, when we are carrying, all combinations overflow, except 0 with 0.

That is, once the carry is “activated”, the 1 I’m carrying cannot come down until it finds 0 and 0.

Example

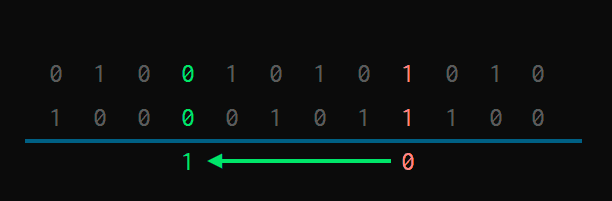
Let’s see it with an example. Suppose we want to add these two 12-bit binary numbers.

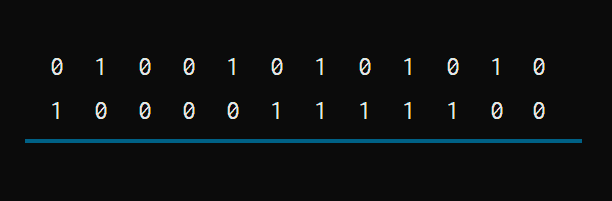
We start from the right, and look for 1 with 1 combinations. That’s where the carry will be activated.

Next, we keep looking until we find a 0 with 0. That’s where the carry can come down.

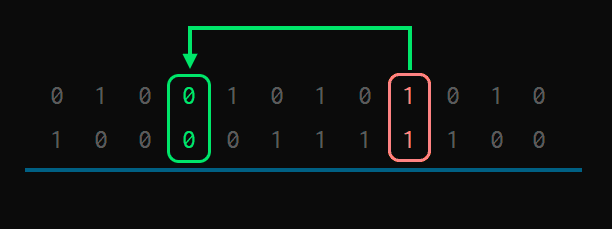
In the end, it’s as if the 1-1 generate a 10. The 0 stays in place, and the 1 goes and goes until it finds a 0-0 where it can come down.

Now, we simply have to fill in the blocks we have defined. In the blocks without carry, we apply the normal rules.

• 0-0 adds 0
• 0-1 or 1-0, one meshes with the other, and gives 1

Or, in other words, in blocks without carry “the 1s rule”.

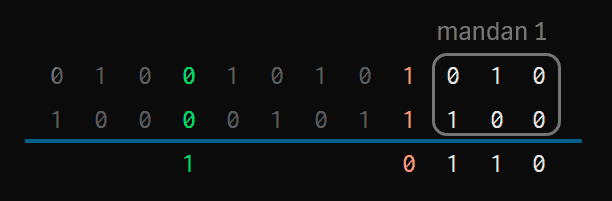
Now we arrive at the next block, which is with carry. Here “the 0s rule”. If there is a 0 in the bits we are adding, the result is 0. Otherwise 1.

And we would continue switching between block with carry, block without carry, until we run out of numbers.

Finally, you can also see it as the blocks without carry being XOR, and those with carry being NXOR.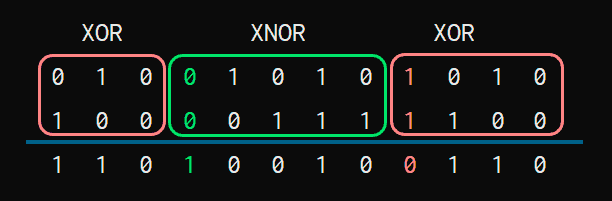

Which is less practical for operating, but allows you to use the Hamlet mnemonic “To Be or Not To Be”, so that in many, many years you will still remember that binary additions are done in XOR and NXOR blocks:

Bonus: How to Add 1 Quickly in Binary

Special bonus, how to quickly add 1 to a binary number. A very simple operation, but since it’s very common it’s good to know how to do it.

Fortunately, adding 1 in binary is “a piece of cake”. Simply

• Traverse the binary number from the right
• Look for the first 0 you find, and change it to 1
• From that position, to the right, all 0s.

For example, if we had to add 1 to 1000011111

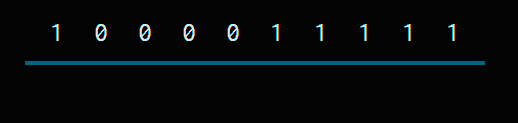
We look for the first 0

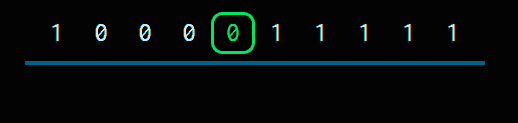
We change it to 1 and, from there to the right, all 0s.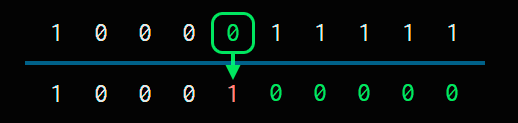

So the result is 1000100000. As you can see, adding one is very fast.