We begin a series aimed at seeing how to make automatic control mechanisms in a processor like Arduino. In this post we will see what it means to control a system. In the next ones, we will see on-off control, and finally, we will end with PID control.
There is no doubt that one of the processors like Arduino is to control systems automatically. But first, what is a controller? What controller can I use? How is a controller implemented?
If you look, you will find a lot of information about it, hundreds of pages full of equations. But the purpose of these entries is to explain it in a simple way (or try), without using a single formula (almost none) and without excessive mathematical formalisms.
Of course, it is not intended to be a rigorous text, as the field is huge (in fact, it was two entire subjects and a specialty in the engineering degree). If you want more details, you can rely on the abundant available literature.
Here we will try to do something that is not so common to find, give an intuitive view of control theory and the motivation behind it, so that it is easily understandable, and without having to use Laplace transforms, root locus, Bode diagrams, or Nyquist theorems.
So we start by asking ourselves.
What is the system to be controlled?
A system is a simplified representation of reality that we abstract in order to work with it, because reality is too complex to work with as a whole. It usually represents a part of reality that we “mentally isolate” (although it can also be totally invented).
A system can be almost anything. The air conditioning in a building, the traction system of a car, the pumping equipment of a tank, an airplane, a spaceship, a robot… even the digestive system of a duck. Anything can be a system for you.
A system, which we will normally call a plant, has one or more inputs that represent actions that we can take. It also has one or more outputs that are the parameters that are observable and measurable. In general, a system has many inputs and outputs, but we are going to simplify it to the most important ones.
In addition, our plant has a certain behavior. That is, performing an action will have a certain consequence on its outputs. Of course, the behavior can be as complicated as you can imagine. It can be nonlinear, have inertia, or even pure delays (a time between when you apply the action and the system “realizes it”), effects between several inputs.
The behavior of the plant can also be abstracted and modeled in a simplified way, in what we know as a transfer function. And we can represent it, for example, by an equation, a block diagram, a graphical or frequency representation, among others.
To make it more “fun” our plant can have disturbances, that is, modifications in the environment that modify its behavior. For example, in the building, the outside temperature will change, in the car, you can go up or down a hill, and in the reservoir, it can start to rain.
In summary, a system is a model of a portion of the universe, with inputs and outputs, whose relationship between them follows a certain behavior and is subject to possible disturbances.
And we represent that like this (and we’re “so cool”).

What is a controller?
The controller is an element that we put in front of the inputs of our plant to act on them in order to ensure that the output has certain characteristics.
For example, you want to control the temperature of a building by acting on the boiler, the speed of the car by acting on the engine, or the level of the tank by acting on the pump.
Logically, the input on which we are going to act must have an influence on the output we want to control. If I am controlling a variable that is completely independent of what I am measuring, I’m not going to do anything!
The controller can be anything from a person to an analog system or a digital system. In automatic systems, we logically refer to some kind of machine that controls the system autonomously without manual intervention.
The controller, represented alongside the system, would look like this.

What characteristics do we want for the output?
The first and most obvious is that the output has a specific value that we will call setpoint. For example, I want the temperature to be 24ºC, the car to go at 80km/h, or the level of the water in a reservoir to be 175m.
Of course, the setpoint does not have to be the same all the time. I may want the temperature to be 17ºC during the night and 24ºC the rest of the time, for the car to go at 50km/h when passing through a town, or to want to empty the reservoir to 160m because I have to supply drinking water to the network.
But, in addition to the setpoint, there are other desired characteristics for the output. In general, I will want the output to be stable in the long term, to converge to the value of the setpoint, to have a fast response time, not to oscillate, not to exceed the setpoint value at any time.
And as it could not be otherwise, or this would be too easy, I will not be able to have them all at once, so I will have to reach a compromise between all of them. Although, if necessary, I may be willing to sacrifice some over others.
For example, maybe you don’t mind that the temperature in a building briefly reaches 24.5ºC, if this means a shorter response time. But if the 180m of water in the reservoir breaks, flooding a town and killing hundreds of people and dogs, maybe exceeding the setpoint is not tolerable and you prefer slow but safe.
Therefore, the desired characteristics for the output depend entirely on your system and what you want to do, and therefore the controller you have to use.
What is a closed loop?
It’s a very nice way of naming a very obvious thing. For a controller to work, it has to have feedback. And what is that? Basically, that the controller has to be able to “see” the output it is trying to control directly or indirectly.
Without feedback, a controller is not a controller, it is more like a “declaration of good intentions blindly”. Imagine that you have to control a variable by turning a lever, and you don’t know what the variable measures. Well, you would have to close your eyes, put the lever in the middle, and hope for the best!
Well, we are clear that to control an output we have to be able to measure it. So we take the output and compare it to the setpoint to see the error we have. We use this error as an input to our controller. We represent this as follows.
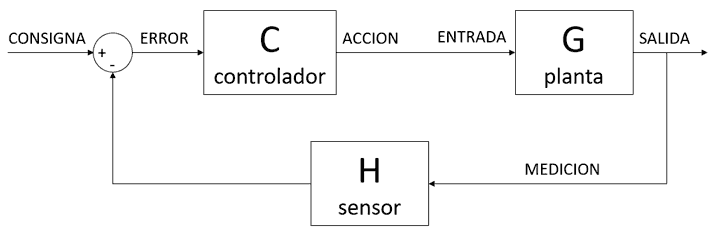
The error between the measurement and the setpoint can be because we have not yet managed to get the output to reach the setpoint, or because the setpoint has changed.
In the end, it is quite intuitive, it makes sense, doesn’t it? So why so much interest in the closed loop? Does the system change a lot by having that feedback branch from the output to the input? Well, yes, all kinds of very interesting things can happen (and some pretty horrible ones).
With feedback, the overall system (controller + plant) behaves completely differently. The output can range from calmly and obediently tending to the setpoint, to oscillating wildly until something breaks.
And the difference between one output (absolute success in your control system) and the other (breakage, dismissal, and possible destruction of the universe) depends entirely on the control you design. Cool, right!?
The intuitive version of the controller
So, what the heck is a controller? A controller is you (in fact, your brain is an excellent controller), who has woken up in the middle of an empty room. In front of you, there is a table with an analog lever that accepts any value between 0 and 100, and on the wall, two huge displays, one blue and one red.
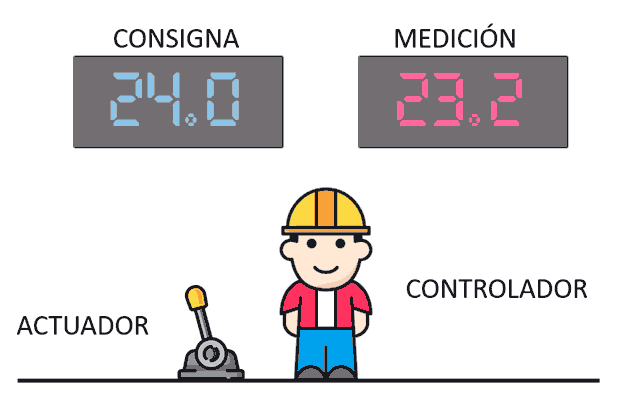
All you know is that the lever in front of you controls, in a certain way, the building’s air conditioning system. The blue number is the setpoint, that is, the temperature your boss asks you to have in the building. And on the red display, the actual temperature measured at this moment.
You don’t know absolutely anything else. You don’t know if it’s a big or small building, how it’s insulated, or the outside temperature, if it’s winter, what time it is, if it’s cloudy, if someone suddenly opens all the windows, if 100 people just entered or if the building has been emptied.
You also don’t know what effect the lever has on the temperature of the building. You don’t know if putting the lever in the middle will turn on the equivalent of two matches, and the temperature will barely change. Or if, on the contrary, you have two spaceship reactors, and at half a lever, you will incinerate everyone.
In short, we are going to assume that you have no prior information about the plant. The only thing we are going to warn you about is that your heating system is sufficient to reach the setpoint, at least under “normal” operation. Because if your actuator has no power, there is little we can do to control the system.
It is clear that if the red display (measurement) were off, it would be much worse. If you only knew they wanted 24ºC, but neither what temperature they are at, nor how the plant is, nor the effect your lever has… as we said before, without feedback, you can only act blindly and cross your fingers.
Things change if the red display lights up. Now, at least, you can compare measurement and setpoint (what we have called error) and maybe we can do something. Could you control the temperature with this information? Certainly, and that is precisely a controller.
How are you going to move the lever, based on what you see on both displays? A lot, a little? That’s the part of designing the controller, determining the response it will make on the lever (actuator) as the values on the displays vary.
What possible strategies can we apply for designing the controller? Many. In the next entry, we will see one of the simplest and most intuitive, the on-off control with hysteresis. In the following, we will see an intuitive approach to the PID controller, one of the most used controllers in the industrial field.
Download the code
All the code from this post is available for download on Github.