In previous entries, we have seen how accelerometers and gyroscopes function as sensors that can be used to determine the orientation of a device.
We also discussed the advantages and limitations of each device, and mentioned that they combine very well because their measurement characteristics complement each other.
In this last entry of the series, we will see IMUs, devices that combine the advantages of both sensors to obtain better functionalities than what we could achieve using an accelerometer or gyroscope independently.
Currently, their low cost has made them common components in a wide variety of everyday devices. There are many manufacturers of IMUs, such as Panasonic, Robert Bosch GmbH, InvenSense, Seiko Epson, Sensonor, STMicroelectronics, Freescale Semiconductor, and AnalogDevices.
We will frequently use them in our electronics and Arduino projects, for example, to determine the direction of movement of a vehicle, the orientation of an actuator, the tilt of a platform, or even as a way to interact with a computer using a glove or a 3D mouse.
What is an IMU?
An Inertial Measurement Unit (IMU) is the generic name for a device that is capable of measuring the velocity, orientation, and acceleration of a system.
In reality, accelerometers and gyroscopes can be considered simple IMUs, but generally, the name IMU is reserved for devices that integrate more than one measurement system.
When talking about IMUs, it is common to refer to the number of degrees of freedom (DOF) it has. The degrees of freedom of a sensor represent the number of independent magnitudes it can measure.
Thus, a 3-axis orthogonal accelerometer is a 3 DOF sensor. Likewise, a gyroscope that measures angles in 3 orthogonal axes is a 3 DOF sensor.
The IMUs we will most often encounter are:
- 6 DOF IMU, combining a 3-axis accelerometer and a 3-axis gyroscope.
- 9 DOF IMU, adding a 3-axis magnetic compass.
- 10 DOF IMU, which adds a barometer for estimating the sensor’s altitude.
As we can see, most IMUs start from a combination of an accelerometer and a gyroscope, being this the most common IMU. The reason is that both devices complement each other well and compensate for each other’s limitations.
- Accelerometers do not have drift in the medium or long term, as they make the absolute measurement of the angle formed by the sensor with the vertical direction marked by gravity. However, they are influenced by the movements of the sensor and noise, so they are not reliable in the short term.
- Gyroscopes work very well for short or abrupt movements, but when using vibration gyroscopes that actually measure angular velocity and obtain the angle by integration over time, they accumulate errors and noise in the measurement, so they have drift in the medium or long term.
Therefore, combining the measurements from both devices allows IMUs to obtain more precise orientation measurements than those of an accelerometer and a gyroscope separately (we will see this next, but first, let’s reflect on what orientation is).
Obtaining Orientation with an IMU
To determine the distribution of an object relative to a base in a three-dimensional space, we must establish its position and orientation. Three parameters are required to determine the relative position and another three to determine its orientation.
In everyday life, we are used to dealing with the position of an object, and we know that there is more than one way to mathematically express its relative position. For example, we can express its coordinates in another base, using Cartesian coordinates (X, Y, Z), cylindrical, or spherical coordinates.
However, we are not as accustomed to working with the parameterization of orientation, as it is mathematically a bit more complex. Just like position, there is more than one way to express the relative orientation of two systems (for example, Euler angles, rotation matrices, or quaternions).
The most widespread and intuitive are the navigation angles, or Tait-Bryan angles, in which the orientation is represented as three orthogonal rotations around the X axis (roll), Y axis (pitch), and Z axis (yaw).
The Tait-Bryan angles are a variation of Euler angles, introduced by the mathematician Leonhard Euler during his study of rigid body mechanics.
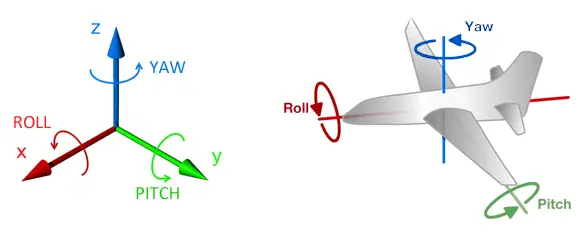
It is common to incorrectly refer to Tait-Bryan angles as Euler angles. The Euler angles are a more general formulation. Another difference is that the Euler angles take the vertical as the origin of measurement, while Tait-Bryan measures angles relative to the horizontal.
The Tait-Bryan angles are intuitive and straightforward. Additionally, they have the advantage of being commutative, meaning the final orientation obtained is independent of the order in which we apply the rotation (something that does not normally occur in rotation representation).
However, they suffer from a major disadvantage known as gimbal lock, which affects all Euler angle systems. When the Y axis rotates +-90º, the X and Z axes coincide, causing the system to degenerate to 2 DOF, which leads to a singular non-differentiable point that can cause stability issues in calculations.
Gimbal lock is such a significant disadvantage that the usual way to represent rotation is through the use of quaternions. Quaternions are an extension of complex numbers introduced by Hamilton in 1843, which use three imaginary units i, j, and k such that,
It is known that complex numbers can be used to represent vectors in the plane. Equivalently, a quaternion allows expressing a vector in three-dimensional space.
To express the rotation of a point, an angle α, around an arbitrary vector with coordinates Ex, Ey, Ez, the resulting quaternion takes the following expression:
Compared to Euler angles, quaternions are simpler to compose and avoid the gimbal lock problem. Compared to rotation matrices, they are more efficient and numerically more stable.
For this reason, quaternions are one of the most common ways to express orientation in computer graphics and will be the preferred method to use when we want to work with orientations in IMUs and Arduino projects.
Signal Filtering in an IMU
To take advantage of the short-term benefits of the gyroscope and the medium to long-term advantages of the accelerometer, it is necessary to combine and filter the raw signal (RAW).
There are several possible filters, with the most famous being the Kalman filter, developed in 1960 by Rudolf E. Kalman. It is considered one of the great discoveries of the 20th century due to its implications in the filtering process in sensors (not just IMUs) and is one of the key contributors to the space race.
In broad strokes, the Kalman filter makes an estimate of the future value of the measurement and then compares the actual value using statistical analysis to compensate for errors in future measurements.
However, the Kalman filter in its general version involves performing complex calculations (see Wikipedia) that represent an excessive implementation and computation time for Arduino.
For this reason, it is common to use a simpler filter called the complementary filter. In reality, the complementary filter can be considered a simplification of the Kalman filter that completely dispenses with statistical analysis.
There are various formulations for a complementary filter. In its simplest expression, the complementary filter can be expressed as:
Where A and B are two constants that can initially be taken as 0.98 and 0.02, respectively. We can calibrate the filter simply by varying the values of A and B as long as we meet the condition that they sum to 1.
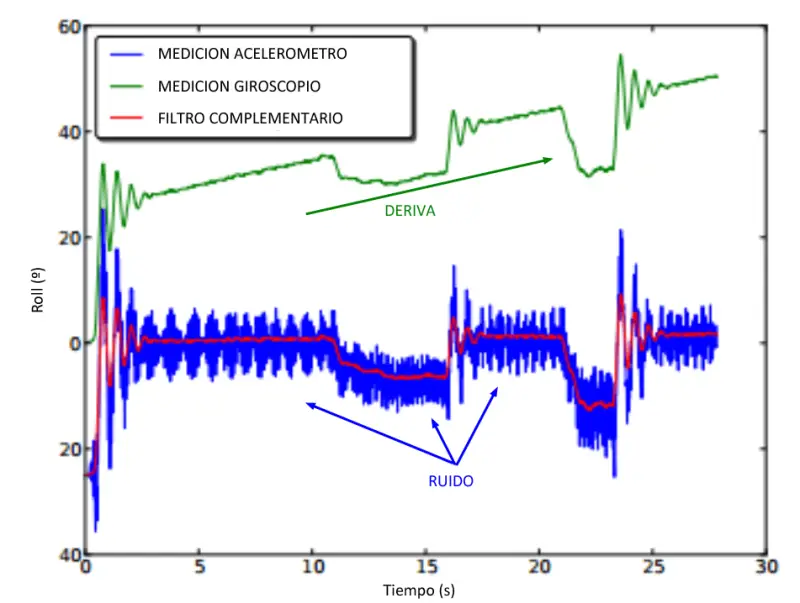
The complementary filter behaves like a high-pass filter for the gyroscope measurement and a low-pass filter for the accelerometer signal. That is, the gyroscope signal dominates in the short term, while the accelerometer signal dominates in the medium and long term, which is exactly what we want to compensate for their advantages and defects.
In most domestic applications, the complementary filter is sufficient and provides values very similar to the Kalman filter, as long as the values of A and B are properly calibrated.
There are more sophisticated versions of the complementary filter, as well as simplified one-dimensional versions of the Kalman filter that can indeed be implemented in Arduino. We will see this in a future advanced entry.
Meanwhile, we will use IMUs such as the MPU6050 and the filters used in our electronics and Arduino projects.
