What are and how to use recursive functions

Recursion is a concept in programming where a function calls itself to solve a problem.

In general, recursion is always somewhat problematic and difficult to understand (especially for those who are starting out in programming).

However, some problems are easier to solve by applying recursion. Not all, by any means. Rather, a small part of the problems.

How Recursion Works

In reality, recursion is easy to implement. Simply we have a function that, at some point, invokes itself.

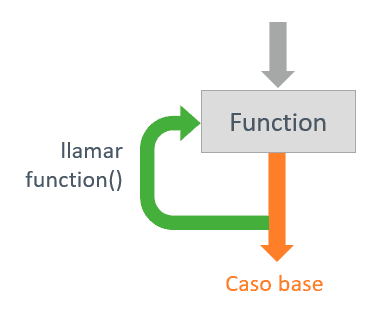
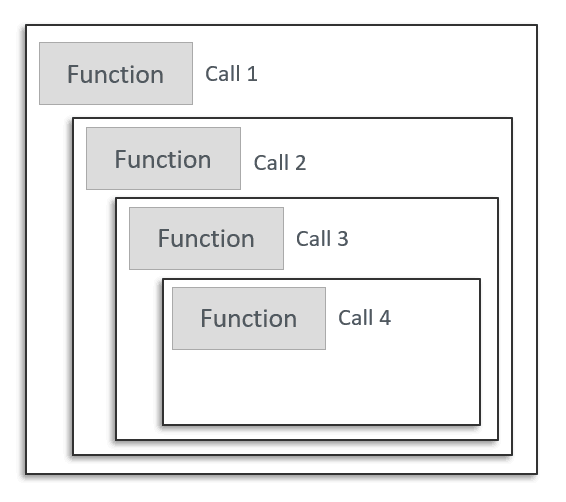
This structure is quite similar to a loop, in that it is a piece of code that executes several times. However, it is not exactly the same. Each call to the function generates its own frame, where local variables are stored.

On the other hand, just as in a loop we have the risk of having an infinite loop, a recursive function can fall into an endless loop.

That is, when does this series of calls stop? At some point, the function has to do “something” that is not calling itself. We will call these cases base cases.

How to Detect Recursive Solutions

How can we detect solutions that could be solved more easily with a recursive approach?

When we have a problem that has several steps, and the result of executing each step leaves us with a problem similar to the previous one.

For example, suppose we have a tray with 5 cakes, and 5 diners. We have to give a cake to each diner.

We take the first cake and do whatever needs to be done. We decide if one is hungrier than another, if they are intolerant to something, if they like chocolate or cream. It doesn’t matter, the point is that we assign a cake.

Now we have one cake assigned, and the problem that remains is the same. But now we have 4 cakes and 4 diners (it’s a very silly example, but it serves to explain recursion).

At each step, the new problem we have is identical to the previous one, but with fewer elements. This indicates that a recursive approach might be simpler.

Examples of Recursive Functions in Different Languages

Let’s look at examples of recursive functions in different languages. For this, we will use a very simple example, the calculation of the factorial of a number.

We can identify that it is a problem suitable to be solved by a recursive approach because, at each step, “what we have left to calculate” is identical to “what we have already calculated”.

That is,

And so on until reaching 1.

Let’s see how we would solve this problem recursively in different languages.

#include <iostream>

// Recursive function to calculate the factorial of a number
int factorial(int n) {
    if (n == 0 || n == 1) {
        return 1; // Base case: factorial of 0 and 1 is 1
    } else {
        return n * factorial(n - 1); // Recursive call
    }
}

int main() {
    int num = 5;
    int result = factorial(num);
    std::cout << "The factorial of " << num << " is: " << result << std::endl;
    return 0;
}

using System;

public class Program {
    // Recursive function to calculate the factorial of a number
    public static int Factorial(int n) {
        if (n == 0 || n == 1) {
            return 1; // Base case: factorial of 0 and 1 is 1
        } else {
            return n * Factorial(n - 1); // Recursive call
        }
    }

    public static void Main() {
        int num = 5;
        int result = Factorial(num);
        Console.WriteLine("The factorial of " + num + " is: " + result);
    }
}

// Recursive function to calculate the factorial of a number
function factorial(n) {
    if (n === 0 || n === 1) {
        return 1; // Base case: factorial of 0 and 1 is 1
    } else {
        return n * factorial(n - 1); // Recursive call
    }
}

let num = 5;
let result = factorial(num);
console.log(`The factorial of ${num} is: ${result}`);

# Recursive function to calculate the factorial of a number
def factorial(n):
    if n == 0 or n == 1:
        return 1  # Base case: factorial of 0 and 1 is 1
    else:
        return n * factorial(n - 1)  # Recursive call

num = 5
result = factorial(num)
print(f"The factorial of {num} is: {result}")

Stack Overflow and Base Cases

We have said that one of the problems with recursive functions is knowing when to stop. We call this the base cases.

If we do not stop the recursive calls, we get into an infinite loop. Each recursive call adds a stack frame to memory, and if these stack frames accumulate without being released, overflow occurs.

Stack overflow occurs when a recursive function calls itself too many times, and the size of the call stack exceeds the set limit.

Let’s see an example that would generate a Stack Overflow.

// Recursive function at risk of Stack Overflow
int recursiveFunctionWithStackOverflow(int n) {
    return recursiveFunctionWithStackOverflow(n + 1); // Recursive call without a base case
}

int main() {
    int num = 0;
    int result = recursiveFunctionWithStackOverflow(num);
    std::cout << "Result: " << result << std::endl; // This will never be reached
    return 0;
}

In the example above, the function recursiveFunctionWithStackOverflow calls itself without a base case, which will cause a stack overflow and an abrupt termination of the program.

Therefore, we need one or more base cases to stop the process of recursive calls.

int recursiveFunctionWithStackOverflow(int n) {
	if(n > 10) return 10; // base case if n > 10
    return recursiveFunctionWithStackOverflow(n + 1);
}

int main() {
    int num = 0;
    int result = recursiveFunctionWithStackOverflow(num);
    std::cout << "Result: " << result << std::endl; // shows 10
    return 0;
}

In this case, we added a conditional that stops the recursive calls. If n > 10 the recursive call does not occur.

Logical Equivalence of Recursion - Iteration

Any recursive function can be converted into a non-recursive function using an iterative approach. This often improves performance and avoids the risk of stack overflow.

For example, the calculation of the factorial in its recursive version

// Recursive function to calculate the factorial of a number
int factorial(int n) {
    if (n == 0 || n == 1) {
        return 1; // Base case: factorial of 0 and 1 is 1
    } else {
        return n * factorial(n - 1); // Recursive call
    }
}

int main() {
    int num = 5;
    int result = factorial(num);
    std::cout << "The factorial of " << num << " is: " << result << std::endl;
    return 0;
}

Can be transformed into an iterative version, for example in the following way,

// Non-recursive (iterative) version to calculate the factorial of a number
int nonRecursiveFactorial(int n) {
    int result = 1;
    for (int i = 1; i <= n; i++) {
        result *= i;
    }
    return result;
}

int main() {
    int num = 5;
    int result = nonRecursiveFactorial(num);
    std::cout << "The factorial of " << num << " is: " << result << std::endl;
    return 0;
}

In this example, we have replaced the recursive factorial function with a non-recursive version that uses a for loop to calculate the result iteratively.

Advantages and Disadvantages of Recursion

Advantages of Recursion

• Ease: In certain cases, implementing a recursive solution may be simpler than an iterative solution.

• Problem Division: Recursion allows us to break down a complex problem into simpler subproblems and solve each subproblem recursively.

• Efficiency for Hierarchical Structures: In problems involving hierarchical structures, such as trees or graphs, recursion can be a natural and efficient way to traverse and manipulate these elements.

Disadvantages of Recursion

• Complex Logic: Some problems may have complex recursive solutions, making them difficult to implement and understand for less experienced programmers.

• Higher memory consumption: Each recursive call creates a new stack frame, which can lead to stack overflow if the number of recursive calls is very large. This can make recursive solutions less efficient in terms of memory consumption compared to iterative approaches.

• Lower efficiency: In some cases, recursive solutions may require more execution time compared to iterative approaches.

• Difficulty in debugging: Recursion can complicate debugging and error tracking, especially when there are multiple recursive calls and the depth of recursion is high.