In this post, we are going to see the necessary equations to calculate an articulated robot on a processor like Arduino. And at the end, we’ll see a library so you never have to do it again!
Solving the position and angles of articulated polygons, especially triangles and quadrilaterals, is important because it frequently appears when working with articulated robots, such as robotic arms, quadrupeds, hexapods, bipeds, etc.
In general, in articulated robots, we know the distance of each side of the articulated polygon and we act on the motors to vary the angle they form between them.
We also know the coordinates of the polygon’s starting point (or we don’t care, if we are going to use coordinates relative to it). On the other hand, each joint node has its own coordinates, with the “end point” being of particular interest because that is typically where we will have the end effector (the robot arm’s gripper, the robot’s leg, etc.).
With this, we have two types of calculations that appear in solving articulated robots:
- Forward Kinematics, where we know the joint angles, and we want to know the end effector’s position.
- Inverse Kinematics, where we know the end effector’s position, and we want to calculate the necessary angles to achieve it.
The latter of these two is more frequent in articulated robots. For example, we know where the ball we want to pick up is or where we want to place a leg, and we need to know what angles to set in the motors to achieve it.
The calculation is not particularly complicated, but it requires a small dose of trigonometry. On the other hand, it should be noted that not all positions will have a solution, while, conversely, some will have more than one (in general, infinite) possible solutions.
Without further ado, let’s see how to solve this problem for the case of articulated triangles and quadrilaterals in 2D and 3D, the most frequent cases we will encounter when working with articulated robots.
2D Articulated Triangle
Forward Kinematics
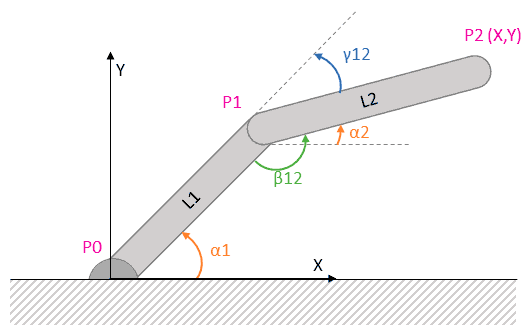
The forward calculation of the end effector’s position (P2), based on the absolute angles of the segments, is obtained simply by projecting onto the X and Y axes, as follows.
Where the relationship between the relative angles between the segments (both interior and exterior) and their absolute angles is calculated using the following expressions.
Inverse Kinematics
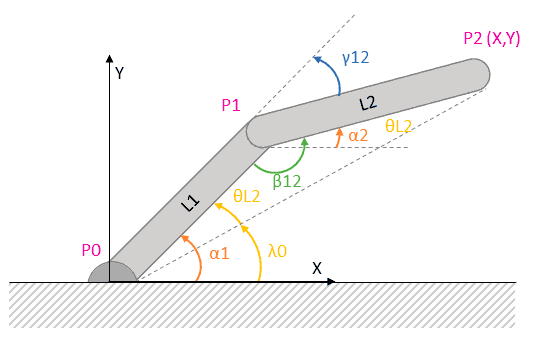
The inverse calculation is equally simple, considering that the two segments form a triangle along with the imaginary line connecting P0 and P2.
We can calculate the distance D from the base P0 to P2, applying the Pythagorean theorem.
With this distance and the lengths of the segments, we can calculate all interior angles of the triangle by applying the generalized law of cosines.
On the other hand, we can calculate the angle that the triangle forms with the X-axis using the following expression.
Finally, we calculate the absolute angle of the first segment by doing.
Knowing the absolute angle of the first segment and the relative angle between them, we can calculate the rest of the relative and absolute angles using the expressions we saw earlier.
Logically, not all positions admit a solution, such as those that exceed the reach of the arms.
Code
Here is a possible code example to solve a 2D articulated triangle on a processor like Arduino.
float L1, L2, D;
float AbsoluteAngle1, AbsoluteAngle2;
float RelativeAngle12;
float TargetX, TargetY;
float Pythagoras(const float& x, const float& y)
{
const float d = sqrt(x * x + y * y);
return d;
}
float SolveInverseCosine(const float& l1, const float& l2, const float& l3)
{
const float angle3 = acos((l1 * l1 + l2 * l2 - l3 * l3) / (2 * l1 * l2));
return angle3;
}
float AbsoluteToRelative(float absolute1, float absolute2)
{
return absolute2 - absolute1 + PI;
}
float RelativeToAbsolute(float relative12, float absolute1)
{
return absolute1 + relative12 - PI;
}
void SolveTriangle(float& x, float& y, float& l1, float& l2, float& d, float& absoluteAngle1, float& absoluteAngle2, float& relativeAngle12)
{
const float angle_0 = atan2(y, x);
d = Pythagoras(x, y);
const float angle_l1 = SolveInverseCosine(d, l2, l1);
const float angle_l2 = SolveInverseCosine(d, l1, l2);
const float angle_D = PI - angle_l1 - angle_l2;
absoluteAngle1 = angle_0 + angle_l2;
relativeAngle12 = angle_D;
absoluteAngle2 = RelativeToAbsolute(relativeAngle12, absoluteAngle1);
}
void SolveDirect(float angle1, float angle2)
{
AbsoluteAngle1 = angle1;
AbsoluteAngle2 = angle2;
SolveDirect();
}
void SolveDirect()
{
RelativeAngle12 = AbsoluteToRelative(AbsoluteAngle1, AbsoluteAngle2);
TargetX = L1 * cos(AbsoluteAngle1) + L2 * cos(AbsoluteAngle2);
TargetY = L1 * sin(AbsoluteAngle1) + L2 * sin(AbsoluteAngle2);
D = Pythagoras(TargetX, TargetY);
}
void SolveReverse()
{
D = Pythagoras(TargetX, TargetY);
float P2x = TargetX;
float P2y = TargetY;
float D0;
SolveTriangle(P2x, P2y, L1, L2, D0, AbsoluteAngle1, AbsoluteAngle2, RelativeAngle12);
}
void Debug()
{
Serial.print(F("Target X:\t"));
Serial.println(TargetX, 4);
Serial.print(F("Target Y:\t"));
Serial.println(TargetY, 4);
Serial.print(F("Abs. Angle 1:\t"));
Serial.println(degrees(AbsoluteAngle1), 4);
Serial.print(F("Abs. Angle 2:\t"));
Serial.println(degrees(AbsoluteAngle2), 4);
Serial.print(F("Rel. Angle 12:\t"));
Serial.println(degrees(RelativeAngle12), 4);
}
void setup()
{
Serial.begin(115200);
while (!Serial) { ; }
L1 = 100; L2 = 50;
Serial.println(F("Solve Direct Relative"));
SolveDirect(radians(55), radians(-20));
Debug();
Serial.println(F("Solve Inverse"));
TargetX = 104.3423;
TargetY = 64.8141;
SolveReverse();
Debug();
}
void loop()
{
// Do nothing
delay(10000);
}
2D Articulated Quadrilateral
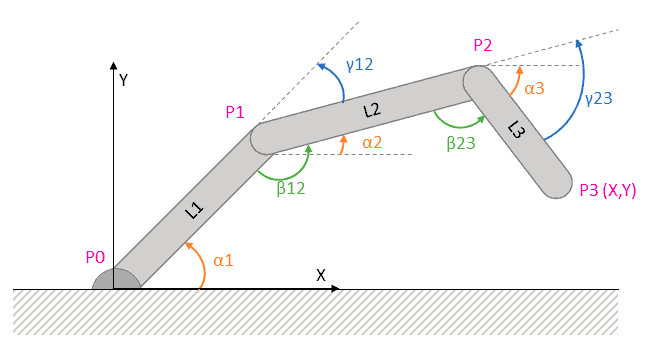
Forward Kinematics
Solving an articulated quadrilateral is similar to the articulated triangle; we simply project the new segment onto the X and Y axes.
Inverse Kinematics
Solving an articulated quadrilateral is no more complex than the triangle in 2D. The new segment adds an additional degree of freedom, so, in general, the problem admits multiple (infinite) solutions.
To solve the system, we must impose a condition (or a relationship between conditions). The usual approach is to provide the absolute angle of the last segment, which corresponds to the end effector’s attack angle.
With the coordinates of point P2, we would solve as in the previous case. As with the triangle, not all positions admit a solution. On the other hand, a solution may exist only for a certain range of end effector angle values.
Frequently, a relationship is established between the end effector’s position and its angle alpha_3, based on making the angle variation during the robot’s movement “smooth”.
Code
Here is a possible code example to solve a 2D articulated quadrilateral on a processor like Arduino.
float L1, L2, L3, D;
float AbsoluteAngle1, AbsoluteAngle2, AbsoluteAngle3;
float RelativeAngle12, RelativeAngle23;
float TargetX, TargetY;
float Pythagoras(const float& x, const float& y)
{
const float d = sqrt(x * x + y * y);
return d;
}
float SolveInverseCosine(const float& l1, const float& l2, const float& l3)
{
const float angle3 = acos((l1 * l1 + l2 * l2 - l3 * l3) / (2 * l1 * l2));
return angle3;
}
float AbsoluteToRelative(float absolute1, float absolute2)
{
return absolute2 - absolute1 + PI;
}
float RelativeToAbsolute(float relative12, float absolute1)
{
return absolute1 + relative12 - PI;
}
void SolveTriangle(float& x, float& y, float& l1, float& l2, float& d, float& absoluteAngle1, float& absoluteAngle2, float& relativeAngle12)
{
const float angle_0 = atan2(y, x);
d = Pythagoras(x, y);
const float angle_l1 = SolveInverseCosine(d, l2, l1);
const float angle_l2 = SolveInverseCosine(d, l1, l2);
const float angle_D = PI - angle_l1 - angle_l2;
absoluteAngle1 = angle_0 + angle_l2;
relativeAngle12 = angle_D;
absoluteAngle2 = RelativeToAbsolute(relativeAngle12, absoluteAngle1);
}
void SolveDirect(float angle1, float angle2, float angle3)
{
AbsoluteAngle1 = angle1;
AbsoluteAngle2 = angle2;
AbsoluteAngle3 = angle3;
SolveDirect();
}
void SolveDirect()
{
RelativeAngle12 = AbsoluteToRelative(AbsoluteAngle1, AbsoluteAngle2);
RelativeAngle23 = AbsoluteToRelative(AbsoluteAngle2, AbsoluteAngle3);
TargetX = L1 * cos(AbsoluteAngle1) + L2 * cos(AbsoluteAngle2) + L3 * cos(AbsoluteAngle3);
TargetY = L1 * sin(AbsoluteAngle1) + L2 * sin(AbsoluteAngle2) + L3 * sin(AbsoluteAngle3);
D = Pythagoras(TargetX, TargetY);
}
void SolveReverse(float absoluteAngle3)
{
AbsoluteAngle3 = absoluteAngle3;
D = Pythagoras(TargetX, TargetY);
float P2x = TargetX - L3 * cos(AbsoluteAngle3);
float P2y = TargetY - L3 * sin(AbsoluteAngle3);
float D0;
SolveTriangle(P2x, P2y, L1, L2, D0, AbsoluteAngle1, AbsoluteAngle2, RelativeAngle12);
RelativeAngle23 = AbsoluteToRelative(AbsoluteAngle2, AbsoluteAngle3);
}
void Debug()
{
Serial.print(F("Target X:\t"));
Serial.println(TargetX, 4);
Serial.print(F("Target Y:\t"));
Serial.println(TargetY, 4);
Serial.print(F("Abs. Angle 1:\t"));
Serial.println(degrees(AbsoluteAngle1), 4);
Serial.print(F("Abs. Angle 2:\t"));
Serial.println(degrees(AbsoluteAngle2), 4);
Serial.print(F("Abs. Angle 3:\t"));
Serial.println(degrees(AbsoluteAngle3), 4);
Serial.print(F("Rel. Angle 12:\t"));
Serial.println(degrees(RelativeAngle12), 4);
Serial.print(F("Rel. Angle 23:\t"));
Serial.println(degrees(RelativeAngle23), 4);
}
void setup()
{
Serial.begin(115200);
while (!Serial) { ; }
L1 = 100; L2 = 50; L3 = 30;
Serial.println(F("Solve Direct Relative"));
SolveDirect(radians(55), radians(-20), radians(-70));
Debug();
Serial.println(F("Solve Inverse"));
TargetX = 114.60289;
TargetY = 36.62342;
SolveReverse(radians(-70));
Debug();
}
void loop()
{
// Do nothing
delay(10000);
}
3D Articulated Triangle
Forward Kinematics
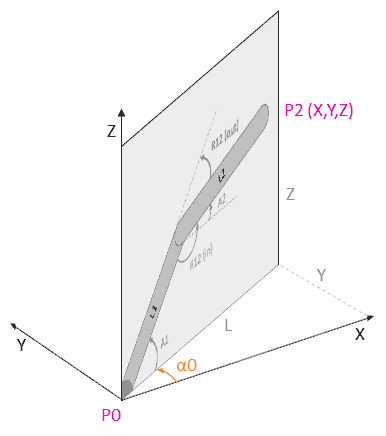
The case of an articulated polygon in 3D can be solved with the same tools as in the 2D case, simply considering that it occurs in a plane rotated by an angle alpha_0 relative to the Z axis.
To convert the coordinates of any point calculated in the plane (Pn’) to its 3D equivalents (Pn), we use the following relationships.
Where sigma is the rotation angle between the plane and the X axis.
Inverse Kinematics
Similarly, we can convert the inverse calculation of a triangle in 3D to a 2D case by projecting onto the equivalent plane.
To do this, we will convert the 3D coordinates of the end effector (P2) to its 2D equivalent (P2’) using the following relationships.
Finally, we would solve as in the 2D case. The angles between segments calculated are the same as in the 3D case. If we wanted to calculate point coordinates, we would use the previous relationships to go from 2D to 3D.
Code
Here is a possible code example to solve a 3D articulated triangle on a processor like Arduino.
float L1, L2, D;
float AbsoluteAngle0, AbsoluteAngle1, AbsoluteAngle2;
float RelativeAngle12;
float TargetX, TargetY, TargetZ;
float Pythagoras(const float& x, const float& y)
{
const float d = sqrt(x * x + y * y);
return d;
}
float Pythagoras(const float& x, const float& y, const float& z)
{
const float d = sqrt(x * x + y * y + z * z);
return d;
}
float SolveInverseCosine(const float& l1, const float& l2, const float& l3)
{
const float angle3 = acos((l1 * l1 + l2 * l2 - l3 * l3) / (2 * l1 * l2));
return angle3;
}
float AbsoluteToRelative(float absolute1, float absolute2)
{
return absolute2 - absolute1 + PI;
}
float RelativeToAbsolute(float relative12, float absolute1)
{
return absolute1 + relative12 - PI;
}
void SolveTriangle(float& x, float& y, float& l1, float& l2, float& d, float& absoluteAngle1, float& absoluteAngle2, float& relativeAngle12)
{
const float angle_0 = atan2(y, x);
d = Pythagoras(x, y);
const float angle_l1 = SolveInverseCosine(d, l2, l1);
const float angle_l2 = SolveInverseCosine(d, l1, l2);
const float angle_D = PI - angle_l1 - angle_l2;
absoluteAngle1 = angle_0 + angle_l2;
relativeAngle12 = angle_D;
absoluteAngle2 = RelativeToAbsolute(relativeAngle12, absoluteAngle1);
}
void SolveDirect(float angle0, float angle1, float angle2)
{
AbsoluteAngle0 = angle0;
AbsoluteAngle1 = angle1;
AbsoluteAngle2 = angle2;
SolveDirect();
}
void SolveDirect()
{
RelativeAngle12 = AbsoluteToRelative(AbsoluteAngle1, AbsoluteAngle2);
float L = L1 * cos(AbsoluteAngle1) + L2 * cos(AbsoluteAngle2);
TargetX = L * cos(AbsoluteAngle0);
TargetY = L * sin(AbsoluteAngle0);
TargetZ = L1 * sin(AbsoluteAngle1) + L2 * sin(AbsoluteAngle2);
D = Pythagoras(TargetX, TargetY, TargetZ);
}
void SolveReverse()
{
AbsoluteAngle0 = atan2(TargetY, TargetX);
D = Pythagoras(TargetX, TargetY, TargetZ);
float Lx = Pythagoras(TargetX, TargetY);
float P2x = Lx;
float P2y = TargetZ;
float D0;
SolveTriangle(P2x, P2y, L1, L2, D0, AbsoluteAngle1, AbsoluteAngle2, RelativeAngle12);
}
void Debug()
{
Serial.print(F("Target X:\t"));
Serial.println(TargetX, 4);
Serial.print(F("Target Y:\t"));
Serial.println(TargetY, 4);
Serial.print(F("Target Z:\t"));
Serial.println(TargetZ, 4);
Serial.print(F("Abs. Angle 0:\t"));
Serial.println(degrees(AbsoluteAngle0), 4);
Serial.print(F("Abs. Angle 1:\t"));
Serial.println(degrees(AbsoluteAngle1), 4);
Serial.print(F("Abs. Angle 2:\t"));
Serial.println(degrees(AbsoluteAngle2), 4);
Serial.print(F("Rel. Angle 12:\t"));
Serial.println(degrees(RelativeAngle12), 4);
}
void setup()
{
Serial.begin(115200);
while (!Serial) { ; }
L1 = 100; L2 = 50;
Serial.println(F("Solve Direct Relative"));
SolveDirect(radians(30), radians(55), radians(-20));
Debug();
Serial.println(F("Solve Inverse"));
TargetX = 90.3631;
TargetY = 52.1711;
TargetZ = 64.8142;
SolveReverse();
Debug();
}
void loop()
{
// Do nothing
delay(10000);
}
Cuadril�tero articulado 3D
Forward
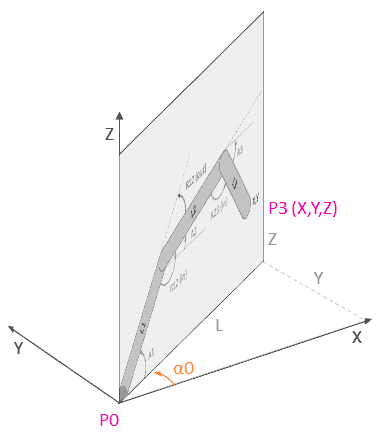
Similarly, for the direct calculation of an articulated quadrilateral in 3D, we project onto a 2D plane using the expressions from the previous section, only considering that this time the angle alpha_0 is.
Inverse
Similarly, an articulated quadrilateral can be solved using the same tools as its 2D equivalent. The only difference is that, in this case, the coordinates of the effects in the equivalent 2D case (P3’) are calculated from the 3D point (P3) according to the following relat
Code
This could be a possible example of code to solve an articulated quadrilateral in 3D on a processor like Arduino.
float L1, L2, L3, D;
float AbsoluteAngle0, AbsoluteAngle1, AbsoluteAngle2, AbsoluteAngle3;
float RelativeAngle12, RelativeAngle23;
float TargetX, TargetY, TargetZ;
float Pythagoras(const float& x, const float& y)
{
const float d = sqrt(x * x + y * y);
return d;
}
float Pythagoras(const float& x, const float& y, const float& z)
{
const float d = sqrt(x * x + y * y + z * z);
return d;
}
float SolveInverseCosine(const float& l1, const float& l2, const float& l3)
{
const float angle3 = acos((l1 * l1 + l2 * l2 - l3 * l3) / (2 * l1 * l2));
return angle3;
}
float AbsoluteToRelative(float absolute1, float absolute2)
{
return absolute2 - absolute1 + PI;
}
float RelativeToAbsolute(float relative12, float absolute1)
{
return absolute1 + relative12 - PI;
}
void SolveTriangle(float& x, float& y, float& l1, float& l2, float& d, float& absoluteAngle1, float& absoluteAngle2, float& relativeAngle12)
{
const float angle_0 = atan2(y, x);
d = Pythagoras(x, y);
const float angle_l1 = SolveInverseCosine(d, l2, l1);
const float angle_l2 = SolveInverseCosine(d, l1, l2);
const float angle_D = PI - angle_l1 - angle_l2;
absoluteAngle1 = angle_0 + angle_l2;
relativeAngle12 = angle_D;
absoluteAngle2 = RelativeToAbsolute(relativeAngle12, absoluteAngle1);
}
void SolveDirect(float angle0, float angle1, float angle2, float angle3)
{
AbsoluteAngle0 = angle0;
AbsoluteAngle1 = angle1;
AbsoluteAngle2 = angle2;
AbsoluteAngle3 = angle3;
SolveDirect();
}
void SolveDirect()
{
RelativeAngle12 = AbsoluteToRelative(AbsoluteAngle1, AbsoluteAngle2);
RelativeAngle23 = AbsoluteToRelative(AbsoluteAngle2, AbsoluteAngle3);
float L = L1 * cos(AbsoluteAngle1) + L2 * cos(AbsoluteAngle2) + L3 * cos(AbsoluteAngle3);
TargetX = L * cos(AbsoluteAngle0);
TargetY = L * sin(AbsoluteAngle0);
TargetZ = L1 * sin(AbsoluteAngle1) + L2 * sin(AbsoluteAngle2) + L3 * sin(AbsoluteAngle3);
D = Pythagoras(TargetX, TargetY, TargetZ);
}
void SolveReverse(float absoluteAngle3)
{
AbsoluteAngle3 = absoluteAngle3;
AbsoluteAngle0 = atan2(TargetY, TargetX);
D = Pythagoras(TargetX, TargetY, TargetZ);
float Lx = Pythagoras(TargetX, TargetY);
float P2x = Lx - L3 * cos(AbsoluteAngle3);
float P2y = TargetZ - L3 * sin(AbsoluteAngle3);
float D0;
SolveTriangle(P2x, P2y, L1, L2, D0, AbsoluteAngle1, AbsoluteAngle2, RelativeAngle12);
RelativeAngle23 = AbsoluteToRelative(AbsoluteAngle2, AbsoluteAngle3);
}
void Debug()
{
Serial.print(F("Target X:\t"));
Serial.println(TargetX, 4);
Serial.print(F("Target Y:\t"));
Serial.println(TargetY, 4);
Serial.print(F("Target Z:\t"));
Serial.println(TargetZ, 4);
Serial.print(F("Abs. Angle 0:\t"));
Serial.println(degrees(AbsoluteAngle0), 4);
Serial.print(F("Abs. Angle 1:\t"));
Serial.println(degrees(AbsoluteAngle1), 4);
Serial.print(F("Abs. Angle 2:\t"));
Serial.println(degrees(AbsoluteAngle2), 4);
Serial.print(F("Abs. Angle 3:\t"));
Serial.println(degrees(AbsoluteAngle3), 4);
Serial.print(F("Rel. Angle 12:\t"));
Serial.println(degrees(RelativeAngle12), 4);
Serial.print(F("Rel. Angle 23:\t"));
Serial.println(degrees(RelativeAngle23), 4);
}
void setup()
{
Serial.begin(115200);
while (!Serial) { ; }
L1 = 100; L2 = 50; L3 = 30;
Serial.println(F("Solve Direct Relative"));
SolveDirect(radians(30), radians(55), radians(-20), radians(-70));
Debug();
Serial.println(F("Solve Inverse"));
TargetX = 99.2490;
TargetY = 57.3014;
TargetZ = 36.62342;
SolveReverse(radians(-70));
Debug();
}
void loop()
{
// Do nothing
delay(10000);
}
Arduino Articulated Library
What if we package this into a library to make it more convenient to use? Absolutely! Here’s an Arduino Articulated library that performs all the aforementioned calculations conveniently and easily. Enjoy