We enter the section of 3D design and printing, and we start properly with the tutorials of 3D design seeing the base, the fundamental ways to represent a 3D object on a computer.
After a few entries dedicated to the Anycubic 3D printer, and having seen the general overview of the 3D printing process in the previous entry, we need to delve deep into the exciting world of 3D.
I can tell you in advance if you are one of those who are looking forward to “melting plastic” you probably won’t find this post so interesting (nor do you need it!). But you don’t want to be “just another” who turns on the printer, plugs in the FreeCAD or downloads an STL, and starts printing without further ado.
You want to become experts in 3D and understand the ins and outs of this exciting world. And for that, it’s best to have a good foundation, which will allow you to understand what you are doing, speak with authority, and also avoid “going around in circles” and unnecessary steps when working with 3D objects.
And it all starts with understanding how that which (and is no more than a “strange entity”) we call “3D object” is presented on a computer. Understanding the differences will be important when we approach the 3D design or printing process.
So in this post, we will see the main ways of representing a 3D object on a computer.
Point clouds
The most basic way to represent a 3D object is a point cloud, where each point is a vertex with coordinates X, Y, Z. Optionally, they may have other characteristics such as color.

Point clouds are important in the world of 3D printing, mainly because 3D scanners return a point cloud.
Due to a simple physical limitation, any sensor (a camera, a probe) must take a finite number of points. Therefore, regardless of the 3D scanner you have, the result of a scan will always be a point cloud.
To convert a point cloud into a 3D mesh or a 3D solid, we will need two additional processes that we call triangulation and reverse engineering, respectively, and which we will see briefly in the next entry.
Mesh models
This is the most common way to represent a 3D model and the one we are most likely used to. They are widely used in animation for video games or movies.
A 3D mesh is formed by a series of points, joined by edges, which in turn form faces. The faces have normals (the direction the face “points” to).
Generally, meshes can have a material, or texture, that is, some type of color representation. Often, the material is an image (bitmap) that is “projected” onto the mesh. The relationship between the flat image and the correspondence on the faces is known as UVW mapping.
Within the representation by 3D meshes, we are going to highlight the following types:
Triangulated meshes
A triangulated mesh, as its name suggests, is simply a mesh formed entirely by triangles. It is the most “simple” mesh that we can conceive, since each face can be contained by three sides/three vertices at a minimum.

Internally, and with very few exceptions, your computer only knows how to represent triangulated surfaces. So, even when we are using any of the other forms of representation, when showing it on the screen, it internally converts it into a triangulated mesh.
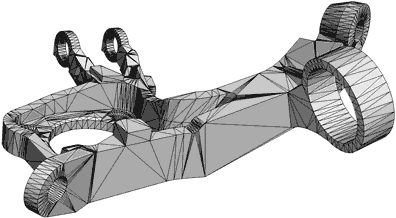
Your graphics card contains circuits specially designed to accelerate the calculations of triangle intersections and light rays, and among them (collisions).
Polygonal meshes (Quads, Ngons)
A polygonal mesh is a mesh formed by polygons with N sides (sometimes called Ngons) is, in a way, an evolution of triangulated surfaces.
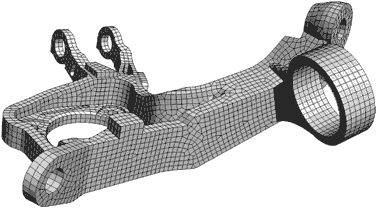
Polygonal meshes are generally simpler and more comfortable to manipulate by the designer, hiding edges that are not really relevant. They are also more comfortable to texture and animate.
On the other hand, Quads are polygons with 4 sides. A 100% quads mesh is a mesh formed entirely by polygons with 4 sides, and they have certain advantages for modeling, especially for Sub-D (which we will see in the next section).
However, even if we handle polygons with N sides, the mesh is internally formed by triangles. The program only “hides” some of the edges and provides us with tools to make it more comfortable to use.
Subdivision Meshes (Sub-D)
Subdivision modeling (sometimes abbreviated Sub-D) is a mesh-based modeling technique that we could currently consider one of the main 3D drawing methods.
Sub-D modeling consists of a mesh, generally polygonal, to which an subdivision algorithm has been applied.
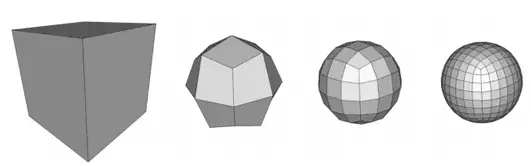
The subdivision algorithm adds additional intermediate points and, according to some criterion (which depends on the algorithm), moves the position of the vertices to give “smoothness” to the mesh. The process can be repeated several times, obtaining different levels of increasing detail.
The designer can modify the vertices of the different levels of subdivision at any time to modify the mesh. In this way, it is possible to achieve both smooth shapes and great detail without having to move a large number of vertices.
There are different subdivision algorithms, among which we can highlight the traditional Loop, the ubiquitous Catmull Clark, or the more modern OpenSubDiv developed by Pixar.
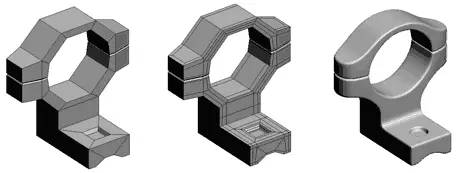
With Sub-D modeling, meshes with a large number of polygons are obtained and, therefore, heavy and slow to process. Normally, subsequently, the high-resolution model is “projected” onto a low-resolution model, and part of the detail becomes part of the “normal map”.
Sub-D modeling has great advantages both from the design point of view, as well as for the application of textures and animation of meshes, so it is one of the main 3D drawing models.

Finally, Sub-D modeling is suitable for modeling complex geometric shapes and models that require many curves, such as organic modeling. On the other hand, it is suitable for models with flat faces or sharp edges.
Surface modeling
Surface modeling is a radically different way of representing three-dimensional objects than the representation meshes, based on mathematical models. These mathematical models allow describing a curved surface in three-dimensional space.
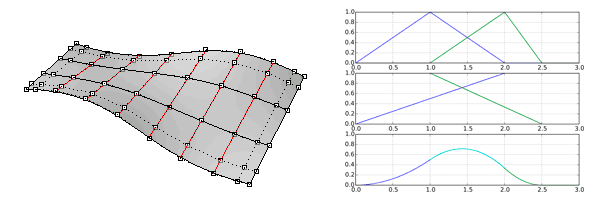
Generally, NURBS surfaces (Non-Uniform Rational B-Splines), or some of its variations such as T-Splines or T-NURCCs (Non-Uniform Rational Catmull-Clark Surfaces with T-junctions) are used.
By using a mathematical model, the surfaces represent a continuous medium instead of a discrete approximation. Thus, the representation of a cylinder has a base and a top circle, instead of a polygon with a certain number of sides. Therefore, they provide great detail and smoothness in the curves.
The typical surface modeling tools are extrusion, revolution, lofting, and rail sweeping. In addition, holes can be defined in the surface and curves can be projected onto the surfaces.

Surfaces, by definition, do not have volume. Therefore, they are not manufacturable/physically realizable. To be able to manufacture them, it will be necessary to apply a thickening operation or close them in a solid.
Except for outstanding exceptions, in general, surfaces cannot be represented by the graphics card. To do so, they are internally converted into a triangulated mesh.
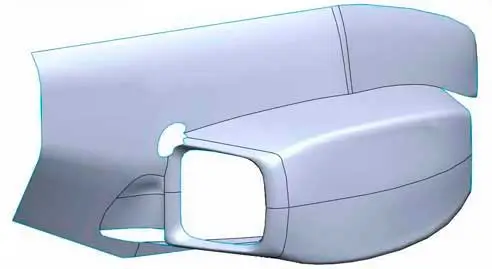
Surface modeling is traditionally linked to the design of parts for manufacturing with complex curves (plastic parts, automotive, etc). It allows representing curved models with ease, while flat faces or edges. However, it is not suitable for models with irregular curves, such as organic modeling.
Solid modeling
Solid modeling is the traditional way of functioning of what we know as CAD software. Solid modeling is, in broad strokes, made up of surface modeling along with the concept of “inside” and “outside”.
For example, when performing an additive extrusion operation (protrusion) or a subtractive extrusion operation (hollowing, hole) the system performs the necessary intersections and normal changes to correctly represent the system.
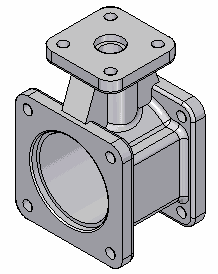
Much of the complexity of solid modeling systems lies in the ways of efficiently calculating these operations (such as K-trees), especially as the complexity of the part increases.
As they are actually based on surface modeling, the basic tools remain the same (extrusion, revolution, lofting, sweeping…). But CAD software incorporates many more operations and tools that allow them to be performed more intuitively and, generally, more similar to physical machining operations (fillet, round, hole, flare).
As we said, solid modeling is traditionally linked to CAD software, and is suitable for representing mechanical parts and manufacturable objects.
Reflection. It is interesting to consider that the relationship occurs in both directions. Solid modeling represents the objects we manufacture well, in part because we use them to manufacture them. As CAD evolves, the complexity of the parts we manufacture also evolves.
These are, in a very summarized way, the ways we have to represent a 3D object on a computer. Each one with its advantages and disadvantages, and more suitable for one type of object than for others.
In case you were wondering, in general, it is not easy to switch from one to another. Something we will see in the next entry on triangulation, retopology, and reverse engineering.
In the next entries, we will see 3D design software, and CAD software that use one or more of these methods for 3D design. In the meantime, if you found the topic interesting and want to add something, or if you have any questions, you can leave us a comment!