A GRAPH is a mathematical data structure that consists of a set of vertices (also called nodes) and a set of edges (also called borders) that connect these vertices.
There are several ways to encode a GRAPH. But, conceptually, a graph is formed by a series of nodes.
Each of the nodes:
- Has its own data “inside”
- Has relationships with other nodes
The relationships between nodes are made through references. Together, this tangle of nodes and relationships forms the GRAPH as a whole.

GRAPHS are an elegant way to model relationships between objects. This structure is one of the most versatile and powerful. You will find it everywhere.
For example, a graph could represent a social network, where the nodes are users and the edges denote friendships or connections. In this way, you could recommend friends or content to users based on the graph.
Another example, a navigation system like Google Maps, where each node represents a location, and the possible relationships are paths. You could find the shortest route using algorithms like Dijkstra.
Or, in a software development project, a graph could represent the dependencies between different modules or packages. This way, you could find circular references, version conflicts, etc.
In summary, you will find graphs everywhere. In fact, other structures like trees or linked lists are simplifications of graphs.
Components of a graph
- Nodes (vertices): These are individual elements in the graph. Each vertex can represent entities like people, places, or any object we are modeling.
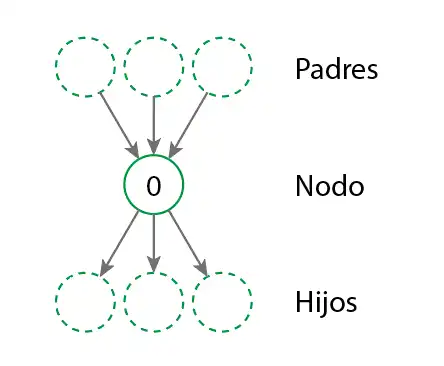
Relationships (edges): These are the connections between the vertices. These edges can be directional or non-directional, depending on the type of relationship we want to represent.
Adjacent node: Nodes that share a relationship with the current node are called adjacent nodes.
Parents and children: When the nodes are directed, nodes with incoming and outgoing relationships are called parents or children.
Types of Graphs
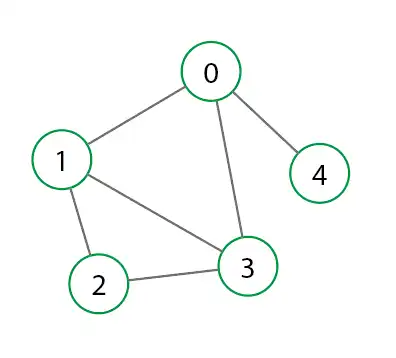
- Undirected Graph: In this type of graph, the edges have no direction. The relationship between two vertices is bidirectional. If A is connected to B, then B is also connected to A.
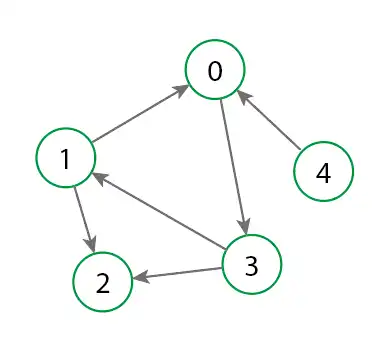
- Directed Graph: In a directed graph, the edges have direction. The relationship between two vertices can be unidirectional. For example, in a route graph, a road may go from A to B but not necessarily from B to A.
- Weighted Graph: In addition to having edges and vertices, a weighted graph assigns a numerical weight to each edge. These weights can represent cost, distance, or any other metric relevant to the particular application.
Graph terminology
Degree of a node: The degree of a node in a graph is the number of incident edges at that node.
Path: A path in a graph is a sequence of nodes connected by edges, where each node in the sequence is connected to the next by an edge.
Cycle: A cycle in a graph is a path that starts and ends at the same node, and that does not repeat any intermediate nodes (except the start/end node).
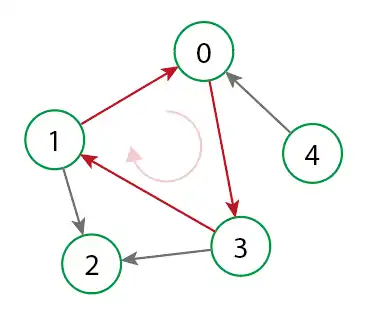
- Connected graph: A graph is connected if there is a path between every pair of nodes in the graph. This means that you can reach from any node to any other node in the graph through a sequence of edges.
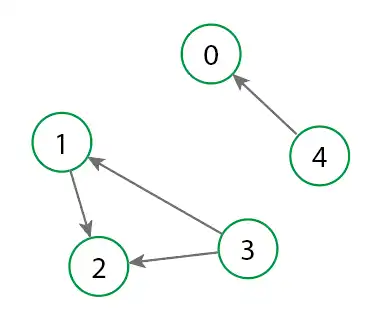
Acyclic graph: An acyclic graph is a graph that does not contain any cycles. In other words, there is no closed path in the graph.
Complete graph: A complete graph is a graph in which every pair of nodes is connected by an edge. This means that there are no isolated nodes in the graph, and that each node is directly connected to all other nodes in the graph.
Example of Graphs in different languages
Graphs are essential for solving a variety of problems in programming, such as finding the shortest path between two points, detecting cycles in a system, or modeling complex relationships.
using System;
using System.Collections.Generic;
public class Node
{
public string Value { get; set; }
public List<Node> Parents { get; set; }
public List<Node> Children { get; set; }
public Node(string value)
{
Value = value;
Parents = new List<Node>();
Children = new List<Node>();
}
public void AddParent(Node parent)
{
Parents.Add(parent);
}
public void AddChild(Node child)
{
Children.Add(child);
}
}
public class Graph
{
private Dictionary<string, Node> Nodes { get; set; }
public Graph()
{
Nodes = new Dictionary<string, Node>();
}
public void AddNode(string value)
{
if (!Nodes.ContainsKey(value))
{
Nodes[value] = new Node(value);
}
}
public void AddEdge(string parentValue, string childValue)
{
AddNode(parentValue);
AddNode(childValue);
Node parent = Nodes[parentValue];
Node child = Nodes[childValue];
parent.AddChild(child);
child.AddParent(parent);
}
public Node GetNode(string value)
{
if (Nodes.ContainsKey(value))
{
return Nodes[value];
}
else
{
return null;
}
}
public void PrintGraph()
{
foreach (var kvp in Nodes)
{
Node node = kvp.Value;
string parents = string.Join(", ", node.Parents.ConvertAll(n => n.Value));
string children = string.Join(", ", node.Children.ConvertAll(n => n.Value));
Console.WriteLine($"Node: {node.Value}, Parents: [{parents}], Children: [{children}]");
}
}
}
class Program
{
static void Main(string[] args)
{
Graph myGraph = new Graph();
myGraph.AddEdge("A", "B");
myGraph.AddEdge("A", "C");
myGraph.AddEdge("B", "D");
myGraph.AddEdge("C", "D");
myGraph.AddEdge("D", "E");
myGraph.AddEdge("E", "F");
myGraph.AddEdge("F", "G");
Console.WriteLine("Graph:");
myGraph.PrintGraph();
Node nodeC = myGraph.GetNode("C");
if (nodeC != null)
{
Console.WriteLine($"\nNode 'C' has parents: {string.Join(", ", nodeC.Parents.ConvertAll(n => n.Value))}");
Console.WriteLine($"Node 'C' has children: {string.Join(", ", nodeC.Children.ConvertAll(n => n.Value))}");
}
else
{
Console.WriteLine("\nNode 'C' does not exist in the graph.");
}
}
}#include <iostream>
#include <vector>
#include <unordered_map>
#include <string>
class Node {
public:
std::string value;
std::vector<Node*> parents;
std::vector<Node*> children;
Node(std::string val) : value(val) {}
void addParent(Node* parent) {
parents.push_back(parent);
}
void addChild(Node* child) {
children.push_back(child);
}
};
class Graph {
private:
std::unordered_map<std::string, Node*> nodes;
public:
void addNode(std::string value) {
if (nodes.find(value) == nodes.end()) {
nodes[value] = new Node(value);
}
}
void addEdge(std::string parentValue, std::string childValue) {
addNode(parentValue);
addNode(childValue);
Node* parent = nodes[parentValue];
Node* child = nodes[childValue];
parent->addChild(child);
child->addParent(parent);
}
Node* getNode(std::string value) {
if (nodes.find(value) != nodes.end()) {
return nodes[value];
}
return nullptr;
}
void printGraph() {
for (auto& kvp : nodes) {
Node* node = kvp.second;
std::cout << "Node: " << node->value << ", Parents: [";
for (auto& parent : node->parents) {
std::cout << parent->value << " ";
}
std::cout << "], Children: [";
for (auto& child : node->children) {
std::cout << child->value << " ";
}
std::cout << "]" << std::endl;
}
}
~Graph() {
for (auto& kvp : nodes) {
delete kvp.second;
}
}
};
int main() {
Graph myGraph;
myGraph.addEdge("A", "B");
myGraph.addEdge("A", "C");
myGraph.addEdge("B", "D");
myGraph.addEdge("C", "D");
myGraph.addEdge("D", "E");
myGraph.addEdge("E", "F");
myGraph.addEdge("F", "G");
std::cout << "Graph:" << std::endl;
myGraph.printGraph();
Node* nodeC = myGraph.getNode("C");
if (nodeC != nullptr) {
std::cout << "\nNode 'C' has parents: ";
for (auto& parent : nodeC->parents) {
std::cout << parent->value << " ";
}
std::cout << "\nNode 'C' has children: ";
for (auto& child : nodeC->children) {
std::cout << child->value << " ";
}
std::cout << std::endl;
} else {
std::cout << "\nNode 'C' does not exist in the graph." << std::endl;
}
return 0;
}class Node {
constructor(value) {
this.value = value;
this.parents = [];
this.children = [];
}
addParent(parent) {
this.parents.push(parent);
}
addChild(child) {
this.children.push(child);
}
}
class Graph {
constructor() {
this.nodes = {};
}
addNode(value) {
if (!this.nodes[value]) {
this.nodes[value] = new Node(value);
}
}
addEdge(parentValue, childValue) {
this.addNode(parentValue);
this.addNode(childValue);
const parent = this.nodes[parentValue];
const child = this.nodes[childValue];
parent.addChild(child);
child.addParent(parent);
}
getNode(value) {
return this.nodes[value] || null;
}
printGraph() {
for (const value in this.nodes) {
const node = this.nodes[value];
const parents = node.parents.map(parent => parent.value).join(", ");
const children = node.children.map(child => child.value).join(", ");
console.log(`Node: ${node.value}, Parents: [${parents}], Children: [${children}]`);
}
}
}
// Creating a graph and adding nodes and edges
const myGraph = new Graph();
myGraph.addEdge("A", "B");
myGraph.addEdge("A", "C");
myGraph.addEdge("B", "D");
myGraph.addEdge("C", "D");
myGraph.addEdge("D", "E");
myGraph.addEdge("E", "F");
myGraph.addEdge("F", "G");
console.log("Graph:");
myGraph.printGraph();
const nodeC = myGraph.getNode("C");
if (nodeC) {
console.log(`\nNode 'C' has parents: ${nodeC.parents.map(parent => parent.value).join(", ")}`);
console.log(`Node 'C' has children: ${nodeC.children.map(child => child.value).join(", ")}`);
} else {
console.log("\nNode 'C' does not exist in the graph.");
}
class Node:
def __init__(self, value):
self.value = value
self.parents = []
self.children = []
def add_parent(self, parent):
self.parents.append(parent)
def add_child(self, child):
self.children.append(child)
class Graph:
def __init__(self):
self.nodes = {}
def add_node(self, value):
new_node = Node(value)
self.nodes[value] = new_node
return new_node
def add_edge(self, parent, child):
if parent not in self.nodes:
self.add_node(parent)
if child not in self.nodes:
self.add_node(child)
self.nodes[parent].add_child(child)
self.nodes[child].add_parent(parent)
def get_node(self, value):
if value in self.nodes:
return self.nodes[value]
else:
return None
def print_graph(self):
for value, node in self.nodes.items():
parents = ', '.join(node.parents)
children = ', '.join(node.children)
print(f"Node: {value}, Parents: [{parents}], Children: [{children}]")
# Creating a graph and adding nodes and edges
my_graph = Graph()
my_graph.add_edge('A', 'B')
my_graph.add_edge('A', 'C')
my_graph.add_edge('B', 'D')
my_graph.add_edge('C', 'D')
my_graph.add_edge('D', 'E')
my_graph.add_edge('E', 'F')
my_graph.add_edge('F', 'G')
# Printing the graph
print("Graph:")
my_graph.print_graph()
# Accessing a specific node
node_c = my_graph.get_node('C')
if node_c:
print("\nNode 'C' has parents:", node_c.parents)
print("Node 'C' has children:", node_c.children)
else:
print("\nNode 'C' does not exist in the graph.")