The HASH SET, also known as HashTables or simply Sets, are unordered collections of unique elements. This means that there cannot be duplicates in a set and the order of the elements does not matter.
Therefore, the only operations that a HASH SET allows are adding, removing, and checking the existence of an element in the collection.
It uses a technique called hashing to organize the elements internally, which allows for fast retrieval and very quick searching of elements.
Properties
| Property | Set |
|---|---|
| Frequency of use | 🔻 |
| Is mutable | ✔️ |
| Is ordered | ❌ |
| Is indexable | ❌ |
| Allows duplicates | ❌ |
When to use a HashSet
The main use of a HASH SET is for efficient searching of elements. Imagine you have a series of trading cards, and you want to know if you already have that card in your collection (the famous “I have, I don’t have” of children).

With a HASH SET, you keep adding each card to the collection. It tells you very quickly (much more than an Array) if you already have that card added previously.
The HASH SET allows you to store elements in a collection to know if you already have that element and retrieve it if necessary. Therefore, the main use is for searching for elements, duplicates, etc.
Finally, the HASH SET has a “sibling,” the DICTIONARY. This operates quite similarly to a HashSet, but with key-value pairs.
Examples of HashSet in different languages
The syntax for using a HashSet can vary depending on the programming language being used.
Next, we will see examples in some popular languages:
HashSet<string> names = new HashSet<string>();
names.Add("Luis");
names.Add("María");
names.Add("Pedro");
foreach (string name in names)
{
Console.WriteLine(name);
}#include <iostream>
#include <unordered_set>
using namespace std;
int main()
{
unordered_set<string> names;
names.insert("Luis");
names.insert("María");
names.insert("Pedro");
for (const string& name : names)
{
cout << name << endl;
}
return 0;
}const names = new Set();
names.add("Luis");
names.add("María");
names.add("Pedro");
for (const name of names)
{
console.log(name);
}names = set()
names.add("Luis")
names.add("María")
names.add("Pedro")
for name in names:
print(name)In the previous examples, we created a HashSet (using the HashSet class in C# and C++, and the Set object in JavaScript and Python) and added several elements to it. Then, we iterated over the elements of the HashSet and displayed them on the screen.
Internal workings Advanced
Internally, a HASH SET works similarly to a dynamic array, but it uses a hash function to generate the numerical indices of the elements.
A hash function is a function that takes an element as input and returns a unique value associated with that element. This unique value is used as an index to store and retrieve the object in the HashSet.
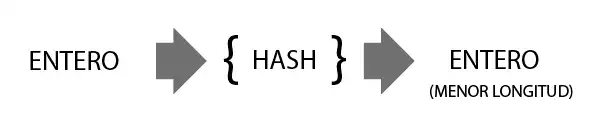
The “grace” of a Hash function is that it is designed to provide unique and uniformly distributed results for each element. It seems very complicated, but a simple example of a hash function could be just calculating the modulo of the element’s value (in binary) with respect to the size of the HASH SET.
When an element is added to the HASH SET, the hash function is applied to the object to determine its storage index. At that position, the element is stored in the position given by its hash function.
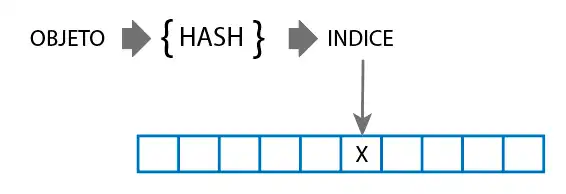
Now, if we need to check if our HASH SET contains an element, we simply calculate the hash function of the element and check if the position is occupied or not. If it is occupied, it means it already contains it, and if it is empty, it means it does not.
If adding elements fills up the HASH SET, since it is a dynamic array, it expands dynamically in a way transparent to the user. Additionally, the hash function is changed for the new size, and all hashes of the stored elements must be recalculated.
This is also the reason why a HashSet has no order. The elements are stored internally “where they belong,” which has nothing to do with the order in which we introduced them.
The hash function ensures that elements are stored and searched for efficiently, as the search is performed directly at the position calculated by the hash function, without needing to traverse all elements.
Efficiency
For a HASH SET, which is a collection where the elements are unordered and do not allow duplicates, the table would look like this:
| Operation | Dictionary |
|---|---|
| Sequential access | ⚫ |
| Random access | 🟢 |
| Add to the beginning | ⚫ |
| Remove from the beginning | ⚫ |
| Add to the end | ⚫ |
| Remove from the end | ⚫ |
| Random insertion | 🟡 |
| Random removal | 🟢 |
| Search | 🟢 |
In the case of the HASH SET, it does not make sense to talk about sequential access, adding to the beginning or removing from the beginning, since the elements are not in a specific order and cannot be accessed directly by index. It also does not make sense to talk about adding or removing from the end since the elements are not in a specific order.
It is possible to add elements “in the order they belong.” That operation is O(1), unless we have to expand the HashSet in which case it is O(n).
The most relevant operation for a HASH SET is the search, which is based on hashing. This allows for quick and constant access to search for elements by their value, which is O(1).
Read more about collection efficiency read more