A TREE is a data structure used to represent hierarchical relationships between elements.
TREES are a reduced version of a DIRECTED GRAPH. Therefore, it consists of interconnected nodes, where each node can have zero or more child nodes.
However, the TREE adds the restrictions that:
- Each node can have only one parent
- It is acyclic
As a result, a TREE results in a structure that originates from a single node, and from there it branches out… just like a tree.

The node at the top is known as the root node. Each parent-child relationship is called a branch. Nodes without children are called leaves. And I think we’ve run out of botanical similes 🌱
TREES are a widely used structure because they allow representing data with hierarchy. By this, we mean that each piece of data can contain other data within it.
Let’s give some examples. The organization of files in a file system follows a tree structure. Each directory can contain files and subdirectories, and these can contain others. And so on.
Another example, a company’s organizational chart could be represented as a tree. Each node represents an employee or a department, and the hierarchical relationships between them are represented by the connections between the nodes.
More examples, the list of products available in an online store. Each node represents a category of products (for example, food, cleaning products, etc.) and the items in each category are the individual products.
Finally, in web development, the Document Object Model (DOM) represents the structure of a web page as a tree. Where each HTML element is a node in the tree, and contains other elements inside it.
In other words, trees are one of the structures you will use most frequently. So it’s advisable to learn how to use them.
Components of a Tree
- Node: A node is a basic entity of a tree that can contain information and references to its child nodes.
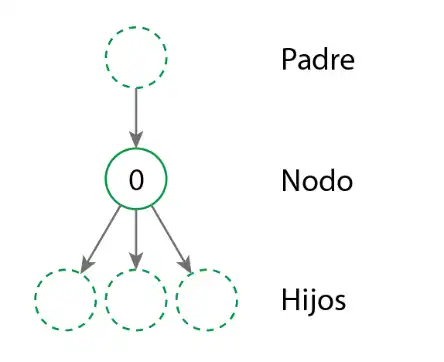
Root Node: It is the main node of the tree, from which all other nodes branch out. A tree can only have one root node.
Leaf Node: A leaf node is one that has no child nodes. In other words, it is the end of a branch in the tree.
Branch: It is each of the relationships between a parent node and its children.
Node Level: The level of a node is its distance from the root node. The level of the root node is 0, and the level of the direct child nodes of the root node is 1, and so on.
Tree Height: The height of a tree is the length of the longest path from the root to a leaf.
Subtree: A subtree is a set of nodes and edges that form a tree within a larger tree. Each node in a tree can be considered the root of a subtree.
Types of Trees
Trees can be classified into several types based on their structure and the restrictions they impose. Some common types of trees include:
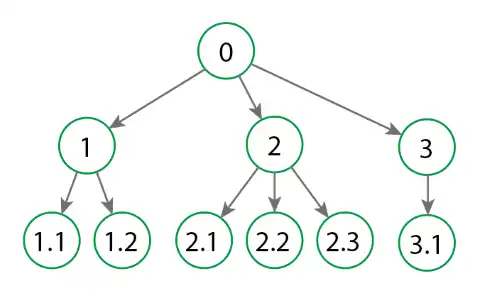
- N-ary Trees: In an N-ary tree, each node can have a variable number of children. This makes it more general than a binary tree.
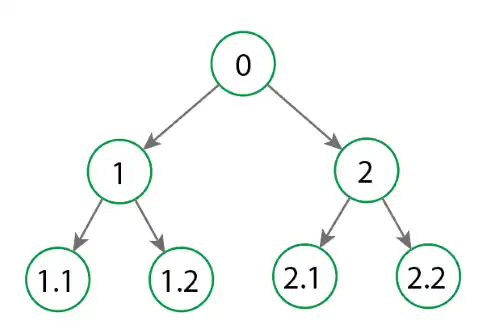
- Binary Trees: A binary tree is one in which each node can have at most two child nodes, usually referred to as left child and right child.
- Binary Search Trees: A binary search tree is a special type of binary tree where for each node, the nodes in the left subtree have values less than the current node, and those in the right subtree have values greater than the current node. This makes it very suitable for searches.
DFS and BFS Search
When working with TREES, the first thing you will need is a way to traverse them. To access their nodes, to search for elements, for everything.
The two common algorithms for traversing trees are:
- DFS (Depth-First Search)
- BFS (Breadth-First Search)
Although these algorithms are called “search”, they are not only used to find a node. They are used to traverse the tree and perform any operation on the nodes we want.
There is no one better than the other; in some problems, DFS will be better, in others, BFS, and in many, it won’t matter which one. Let’s take a look 👇
Depth-First Search (DFS)
This DFS method traverses the tree depth-wise, visiting all descendants of a node before moving to the next sibling.
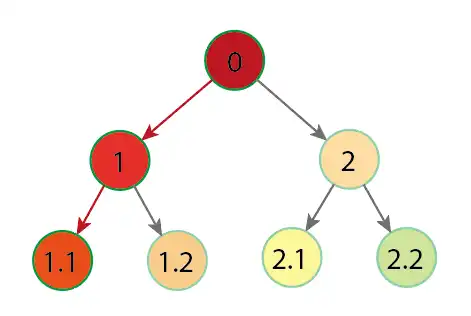
That is, suppose we want to perform an action on a node. I’m going to call it the action 🎇. For example, we want to initialize the value of each node, or search, or whatever.
DFS is called “depth-first” because it prioritizes going down vertically. So it takes the root of the tree and goes down as far as it can. Then it backtracks, moves horizontally, and goes down as much as it can again.
Typically, DFS is implemented as a straightforward recursive function:
- Start from the root node
- Call the recursive function 🔁 for each of its children
- Then execute
the action🎇 on the node
recursive_DFS(node, action)
{
// Traverse all the children of the current node
node.childs.foreach(child => recursive_DFS(child, action));
// After visiting all children, apply the action to the current node
action(node);
}Breadth-First Search (BFS)
The BFS method traverses all nodes at one level, before moving to the next level, visiting all neighbors of a node before continuing to the next level.
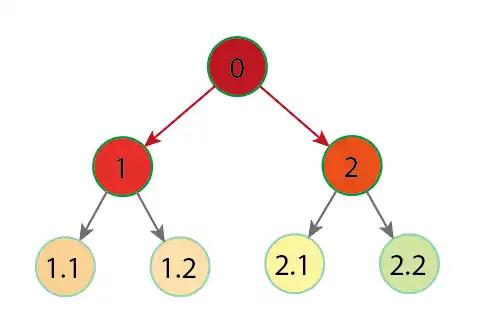
BFS is called “breadth-first” because it prioritizes expanding horizontally. So it takes the root of the tree and goes through all its children. Then it moves to the next level, processing all nodes. It goes down levels until it finishes.
To implement a BFS, we generally use an auxiliary collection, like a list or a queue. The algorithm is:
- Start from the root node, enqueue it
- While the queue is not empty
- Dequeue the first node, and execute
the action🎇 on it - Enqueue all the children of this node
- Dequeue the first node, and execute
recursive_BFS(node, action)
{
queue = new Queue(); // Create a queue to store the nodes to visit
queue.enqueue(node); // Add the root node to the queue
while (!queue.isEmpty()) { // While there are nodes in the queue
current = queue.dequeue(); // Dequeue the first node
action(current); // Apply the action to the current node
// Enqueue the children of the current node
current.childs.foreach(child => queue.enqueue(child));
}
}Tree Example in Different Languages
Let’s see how to implement a non-binary tree in different programming languages:
using System;
using System.Collections.Generic;
class Node
{
public int Value { get; set; }
public List<Node> Children { get; set; }
public Node(int value)
{
Value = value;
Children = new List<Node>();
}
public void AddChild(Node child)
{
Children.Add(child);
}
public override string ToString()
{
return $"Node Value: {Value}";
}
}
class Tree
{
public Node Root { get; set; }
public Tree()
{
Root = null;
}
public void PrintTree(Node node, string indent = "")
{
if (node == null) return;
Console.WriteLine(indent + node.ToString());
if (node.Children != null)
{
foreach (var child in node.Children)
{
PrintTree(child, indent + " ");
}
}
}
public Node Search(int value, Node node)
{
if (node == null) return null;
if (node.Value == value) return node;
foreach (var child in node.Children)
{
var foundNode = Search(value, child);
if (foundNode != null) return foundNode;
}
return null;
}
public void DFS(Node node)
{
if (node == null) return;
Console.WriteLine(node.Value);
if (node.Children != null)
{
foreach (var child in node.Children)
{
DFS(child);
}
}
}
public void BFS()
{
if (Root == null) return;
Queue<Node> queue = new Queue<Node>();
queue.Enqueue(Root);
while (queue.Count > 0)
{
Node current = queue.Dequeue();
Console.WriteLine(current.Value);
foreach (var child in current.Children)
{
queue.Enqueue(child);
}
}
}
}
class Program
{
static void Main(string[] args)
{
Tree tree = new Tree();
tree.Root = new Node(1);
tree.Root.AddChild(new Node(2));
tree.Root.AddChild(new Node(3));
tree.Root.Children[0].AddChild(new Node(4));
// Print the tree
Console.WriteLine("Tree:");
tree.PrintTree(tree.Root);
// Search for a value in the tree
int valueToFind = 4;
Node foundNode = tree.Search(valueToFind, tree.Root);
if (foundNode != null)
{
Console.WriteLine($"\nFound the node with value {valueToFind}: {foundNode}");
}
else
{
Console.WriteLine($"\nNode with value {valueToFind} not found.");
}
// DFS
Console.WriteLine("\nDepth-First Traversal (DFS):");
tree.DFS(tree.Root);
// BFS
Console.WriteLine("\nBreadth-First Traversal (BFS):");
tree.BFS();
}
}#include <iostream>
#include <queue>
#include <vector>
class Node {
public:
int value;
std::vector<Node*> children;
Node(int val) : value(val) {}
void addChild(Node* child) {
children.push_back(child);
}
};
class Tree {
public:
Node* root;
Tree() : root(nullptr) {}
void printTree(Node* node, std::string indent = "") {
if (node == nullptr) return;
std::cout << indent << "Node Value: " << node->value << std::endl;
for (auto child : node->children) {
printTree(child, indent + " ");
}
}
Node* search(int value, Node* node) {
if (node == nullptr) return nullptr;
if (node->value == value) return node;
for (auto child : node->children) {
Node* foundNode = search(value, child);
if (foundNode != nullptr) return foundNode;
}
return nullptr;
}
void DFS(Node* node) {
if (node == nullptr) return;
std::cout << node->value << std::endl;
for (auto child : node->children) {
DFS(child);
}
}
void BFS() {
if (root == nullptr) return;
std::queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* current = q.front();
q.pop();
std::cout << current->value << std::endl;
for (auto child : current->children) {
q.push(child);
}
}
}
};
int main() {
Tree tree;
tree.root = new Node(1);
tree.root->addChild(new Node(2));
tree.root->addChild(new Node(3));
tree.root->children[0]->addChild(new Node(4));
// Print the tree
std::cout << "Tree:" << std::endl;
tree.printTree(tree.root);
// Search for a value in the tree
int valueToFind = 4;
Node* foundNode = tree.search(valueToFind, tree.root);
if (foundNode != nullptr) {
std::cout << "\nFound the node with value " << valueToFind << ": Node Value: " << foundNode->value << std::endl;
} else {
std::cout << "\nNode with value " << valueToFind << " not found." << std::endl;
}
// DFS
std::cout << "\nDepth-First Traversal (DFS):" << std::endl;
tree.DFS(tree.root);
// BFS
std::cout << "\nBreadth-First Traversal (BFS):" << std::endl;
tree.BFS();
// Free memory
delete tree.root->children[0]->children[0];
delete tree.root->children[0];
delete tree.root->children[1];
delete tree.root;
return 0;
}class Node {
constructor(value) {
this.value = value;
this.children = [];
}
addChild(child) {
this.children.push(child);
}
}
class Tree {
constructor() {
this.root = null;
}
printTree(node, indent = "") {
if (node === null) return;
console.log(indent + "Node Value: " + node.value);
for (let child of node.children) {
this.printTree(child, indent + " ");
}
}
search(value, node) {
if (node === null) return null;
if (node.value === value) return node;
for (let child of node.children) {
let foundNode = this.search(value, child);
if (foundNode !== null) return foundNode;
}
return null;
}
DFS(node) {
if (node === null) return;
console.log(node.value);
for (let child of node.children) {
this.DFS(child);
}
}
BFS() {
if (this.root === null) return;
let queue = [this.root];
while (queue.length > 0) {
let current = queue.shift();
console.log(current.value);
for (let child of current.children) {
queue.push(child);
}
}
}
}
// Create the tree
let tree = new Tree();
tree.root = new Node(1);
tree.root.addChild(new Node(2));
tree.root.addChild(new Node(3));
tree.root.children[0].addChild(new Node(4));
// Print the tree
console.log("Tree:");
tree.printTree(tree.root);
// Search for a value in the tree
let valueToFind = 4;
let foundNode = tree.search(valueToFind, tree.root);
if (foundNode !== null) {
console.log(`\nFound the node with value ${valueToFind}: Node Value: ${foundNode.value}`);
} else {
console.log(`\nNode with value ${valueToFind} not found.`);
}
// DFS
console.log("\nDepth-First Traversal (DFS):");
tree.DFS(tree.root);
// BFS
console.log("\nBreadth-First Traversal (BFS):");
tree.BFS();class Node:
def __init__(self, value):
self.value = value
self.children = []
def add_child(self, child):
self.children.append(child)
class Tree:
def __init__(self):
self.root = None
def print_tree(self, node, indent=""):
if node is None:
return
print(indent + "Node Value: " + str(node.value))
for child in node.children:
self.print_tree(child, indent + " ")
def search(self, value, node):
if node is None:
return None
if node.value == value:
return node
for child in node.children:
found_node = self.search(value, child)
if found_node is not None:
return found_node
return None
def dfs(self, node):
if node is None:
return
print(node.value)
for child in node.children:
self.dfs(child)
def bfs(self):
if self.root is None:
return
queue = [self.root]
while queue:
current = queue.pop(0)
print(current.value)
for child in current.children:
queue.append(child)
# Create the tree
tree = Tree()
tree.root = Node(1)
tree.root.add_child(Node(2))
tree.root.add_child(Node(3))
tree.root.children[0].add_child(Node(4))
# Print the tree
print("Tree:")
tree.print_tree(tree.root)
# Search for a value in the tree
value_to_find = 4
found_node = tree.search(value_to_find, tree.root)
if found_node is not None:
print(f"\nFound the node with value {value_to_find}: Node Value: {found_node.value}")
else:
print(f"\nNode with value {value_to_find} not found.")
# DFS
print("\nDepth-First Traversal (DFS):")
tree.dfs(tree.root)
# BFS
print("\nBreadth-First Traversal (BFS):")
tree.bfs()