Explicación del teorema de muestreo de Nyquist sin ecuaciones

Nueva entrada de esta serie que me encanta de explicar conceptos de matemáticas e ingeniería sin ecuaciones. En esta ocasión nos toca ver, el Teorema de muestreo de Nyquist - Shannon.

Para los que no lo conozcáis, el teorema de muestreo fue formulado por Nyquist en 1928, y demostrado por Shannon en 1949, y es una de las piedras fundamentales del tratamiento digital de señales.

La formulación más conocida del teorema es que para poder reconstruir una señal muestreada, la frecuencia de muestreo debe ser superior al doble del ancho de banda.

Y ahora normalmente vendría un rollo matemático para demostrar esto. Cosa que, precisamente, NO es el objetivo de esta entrada, sino todo lo contrario.

No me entendáis mal, me encantan las ecuaciones. Pero si para explicar algo necesitan dos folios de matemáticas, igual tu profe no lo entendía del todo (y tu corres el riesgo de olvidarlo en un ‘plis’).

Entonces, de que va toda esta mística y artículos interminables sobre el “teoooremaaa de muestreeeeo”. Pero, antes de llegar a eso, necesitamos empezar por recordar qué es una señal muestreada.

Señales muestreadas

Supongamos una señal “real” del mundo físico, como por ejemplo una señal de audio o una electromagnética. En general, estas señales “reales” son variaciones en la medición de una magnitud. Salvo contadas (y rebuscadas) excepciones las señales físicas siempre son analógicas.

En este contexto, alejados un momento de la pizarra y el libro de matemáticas, por “real” y analógico nos referimos a señales no continuas, no periódicas, con infinito grado de detalle y hasta su buen puntito de ruido. Una auténtica fiesta de señal, vamos.

Por ejemplo, que lo siguiente es una señal de audio que ha captado con un micrófono.

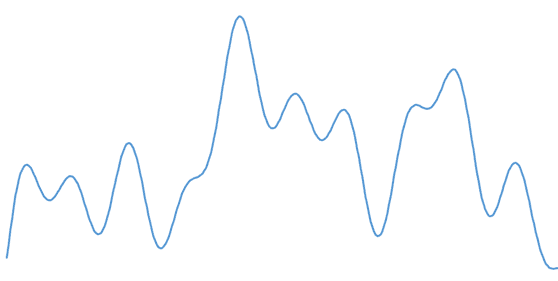
Si yo quiero almacenar digitalmente esta señal analógica “real”, no me cabe. Necesitaría memoria infinita para almacenar su infinito grado de detalle. Así que de alguna forma tengo que simplificarla. Y simplificar, casi siempre, supone perder información.

La forma más sencilla e intuitiva de digitalizar nuestra señal “real” es muestrearla, es decir, tomar mediciones a intervalos regulares y almacenarlos. Esta lista de números, es nuestra señal digital.

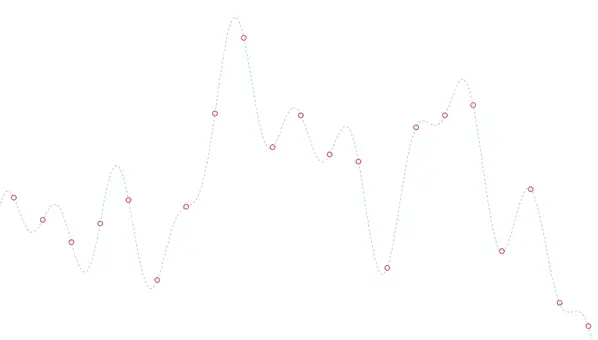
Luego, si tengo que reconstruir la señal analógica a partir de los datos tengo diversas formas, como “jugar a unir los puntos”, o interpolaciones más sofisticadas o menos, en función de lo que me quiera matar la cabeza y cuanta potencia de cálculo tenga.

Una característica evidente del proceso de muestro es que cuanto más cerca tenga los puntos, es decir, mayor sea mi frecuencia de muestreo, captaré más detalles de la señal.

Y al revés, si los voy separando más y más, acabaré con una patata de señal digital, porque si mi frecuencia de muestreo es muy pequeña frente a la de la señal pierdo mucha información. Entre dos puntos puede haber un pico, una curva suave, 20 oscilaciones… un camello, un elefante, cualquier cosa (que, por otro lado, puede que me interese, o no).

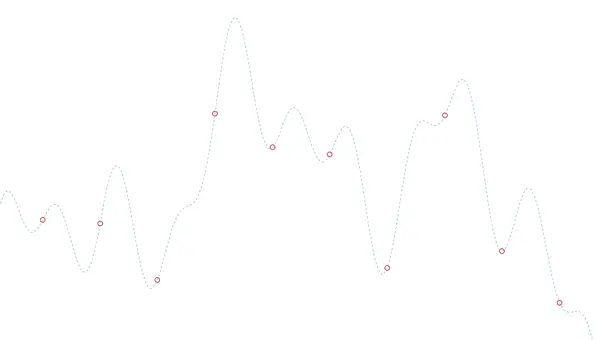
Pues esto mismo ya les preocupaba a Nyquist, Shannon (y otros) hace 100 años, y es de lo que va el teorema de muestreo, de cómo afecta a la calidad de la señal muestreada la separación entre los puntos.

Espectro de la señal

Nuestra señal “real” es continua, infinitamente detallada y, además, inventada. Yo dibujaré una, y tú otra distinta. Así que pocas conclusiones vamos a poder sacar así.

Para sacar conclusiones teóricas relevantes es conveniente que nos traslademos al dominio frecuencial, es decir, que vamos la señal en una representación alternativa como un sumatorio de señales senoidales.

Para pasar el dominio temporal al frecuencial empleamos la Transformada integral de Fourier. En concreto, usaremos alguna de sus versiones como la DFT (Discrete Fourier Transform) y el algoritmo FFT (Fast Fourier Transform). Pero, para nuestra explicación, es lo mismo.

Esta transformada nos permite tratar (o ver, o concebir) nuestra señal de otra forma, pero sin cambiarla (por eso es una transformada, no una cambiada de Fourier). Simplemente, en lugar de tratarla una función que la magnitud de la señal en cada instante de tiempo, ahora la tratamos como una función que codifica la amplitud de sus componentes frecuenciales.

Al pasar al dominio frecuencial nuestra señal, obtenemos esta función que llamaremos el espectro de la función. Si nuestra función “real” era continua, no periódica, bla bla bla… , su espectro será también es continuo, no periódico, con ruido, bla bla bla.

¿Pues vaya gracia no? ¿Entonces para que hemos hecho todo esto? Porque ahora, si podemos saber que le pasa a una señal senoidal de una determinada frecuencia cuando la muestreamos, podemos deducir que le va a pasar a la señal “real” (o al menos a parte de ella) cuando la muestreemos.

Pues vamos, allá, vamos a coger nuestra señal del punto anterior y hacerle una transformada de Fourier y vemos… que os he timado. En realidad, la he generado con la suma de cuatro señales seno, con frecuencias y amplitudes inventadas

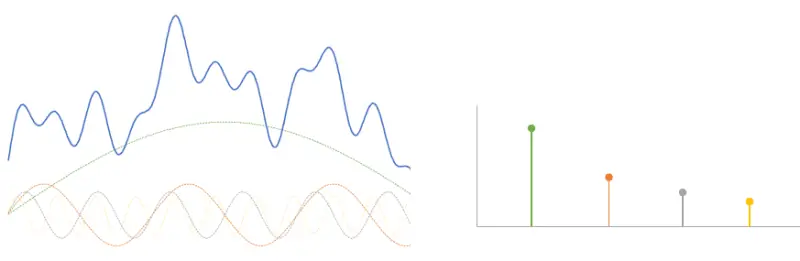
Bueno, que esperabais, ya os he dicho que no se puede almacenar una señal “real”. Y nos ha servido para poder visualizar sus componentes frecuenciales. Pero tener en cuenta que en una señal “real” su espectro sería continuo, y en lugar de cuatro puntos, tendríamos una curva continua.

Representación mediante fasores

El apartado anterior ha servido para concluir que vamos a trabajar con la señal en su dominio frecuencial. De esta forma, sólo necesitamos trabajar con señales senoidales para extraer consecuencias válidas sobre cómo afecta el muestreo a las señales “reales”.

Toca otra herramienta más, que es el tratamiento de las señales senoidales mediante su representación fasorial. ¿Y esto que narices es ahora? Una pelota que gira, pero es que los nombres ayudan poco a que esto parezca sencillo.

Os sonará del instituto que un senoide (seno, coseno) es en realidad la proyección de un punto que está girando en torno a un centro. De hecho, cada vez que aparece en la naturaleza un fenómeno que sigue un patrón senoidal, es porque está relacionado con “algo” que gira, y lo estás mirando mal. Pero eso es otro debate.

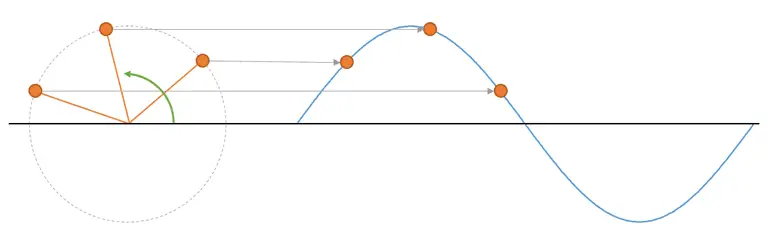
Esto es una representación fasorial y simplifica muchísimo el trabajo con senoides. El radio de giro del fasor respecto al centro es la amplitud de la onda, y la frecuencia de la senoide es la frecuencia con la que gira el fasor, que es equivalente a su velocidad de giro.

Con esto en mente, tenemos las herramientas suficientes para entender el teorema del muestreo.

El problema del muestreo

Recentrando el tema, el problema del muestreo se resume a groso modo en es saber si podemos reconstruir una señal a partir de los “puntos” muestreados, o al menos que consecuencias tiene el proceso en la señal muestreada respecto a la original.

Al pasar al dominio frecuencial, el problema ha pasado a ser, dada esa serie de puntos, ¿eres capaz de decirme las señales senoidales que mejor ajustan a esa serie de puntos? Leñes.. ¡es incluso peor que antes! ¿¡Cómo voy a saber eso?!

No, ya no es tan difícil. Si trabajamos en fasores, la pregunta acaba siendo, ¿eres capaz de decirme para cada una de las pelotas siguientes, su frecuencia y su radio de giro? Y eso es muy fácil, porque cada pelota gira a una velocidad distinta.

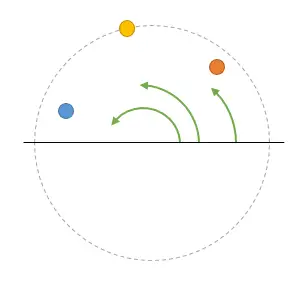
Como soy capaz de discriminar fácilmente cada “pelota” (componente frecuencial) simplemente porque van a velocidades distintas, puedo centrarme el análisis de sólo una sola frecuencia, y el resto de análisis será similar para todos los componentes.

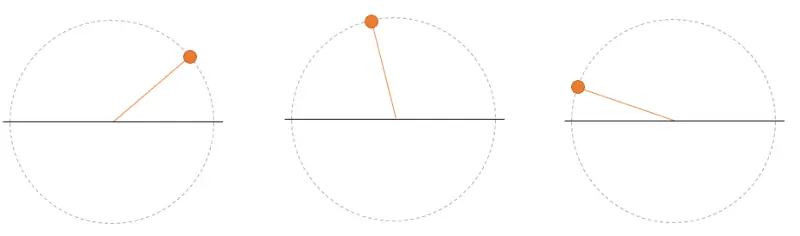
Así que ya sólo me importa, por ejemplo, la pelota roja. Tras el muestreo tengo “imágenes estáticas” (muestras) de la pelota en su movimiento. Solo tenemos que calcular su velocidad angular, para determinar el componente frecuencial.

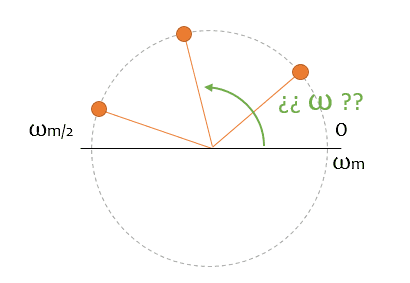
¡Y eso es muy fácil! ¿O no? Pista, si fuera tan fácil no estaríamos aquí. Esto está a punto de ponerse interesante.

Armónicos fundamentales

Primera dificultad, pero no demasiado problemática. Tú ves la siguiente pelota (vamos a llamarle fasor a partir de ahora, ¿vale?) girando, y calcular la velocidad de giro es trivial. ¿No?

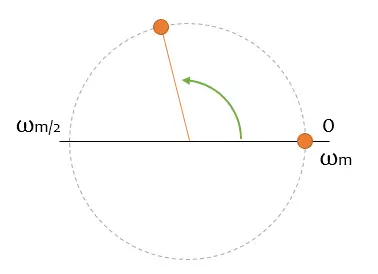
Pues sí y no. Porque tú solo tienes dos imágenes fijas, y no sabes si entre ambas, el fasor ha dado 10, 20, o tres millones de vueltas (¿recordáis? un camello, un elefante…) En todos los casos, la pelota estaría en el mismo punto en la segunda foto.

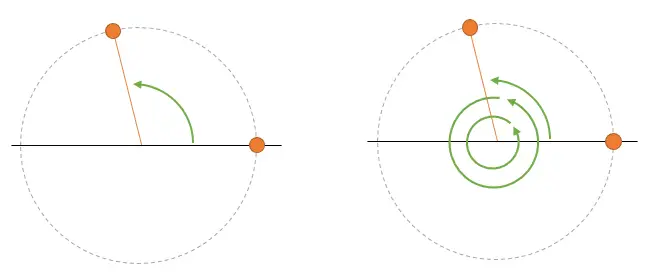
Ese es un primer problema del muestreo, que tienes una incertidumbre sobre que armónico estás representando. En general, no es un gran problema porque tú sabes que estás muestreando a una frecuencia Wm, así que toda frecuencia superior es “razonable” asumido que lo vas a perder.

Pero, es importante que tengáis en la mente para los siguientes apartados, que la velocidad (frecuencia) que voy a asumir que quieres cuando hagamos la reconstrucción es la menor de las posibles.

Explicación del teorema del muestreo

Ya llegamos al “cogollo” de la entrada. ¿Qué es lo que pasa cuando incrementamos la frecuencia del componente en relación a la frecuencia de muestreo? (bien sea porque aumentamos la frecuencia del componente, o porque reducimos la frecuencia de muestreo).

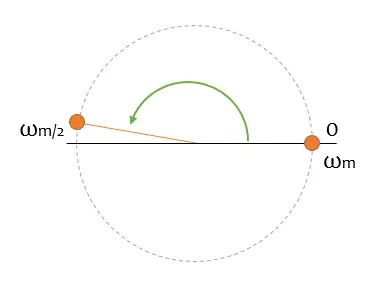
Bien, de momento sin problemas. Aumentemos la velocidad de giro del fasor un poco más, hasta que pase el eje de abcisas. ¿Qué pasará entonces?

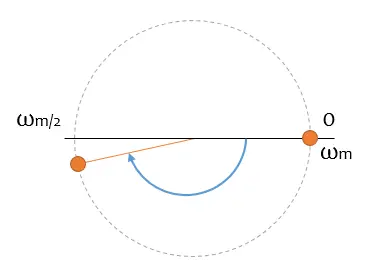
¡Anda la leche! Esperabas que la flecha verde se hiciera un poco más grande, pero en lugar de eso ha aparecido una azul. ¿Ah, que no había dicho que los fasores pueden girar en ambos sentidos? Pues si, giran en los dos sentidos.

Y recordar que, del apartado anterior, os he dicho que os iba a decir la velocidad más baja de todas las posibles. En cuanto pasas el eje de abcisas, pienso que está girando en sentido contrario.

Por fin llegamos a nuestra demostración sin ecuaciones. Si quieres que reconstruya una frecuencia, necesito tener al menos dos muestras en la misma mitad del círculo. Es decir, que su frecuencia tiene que ser inferior, a la mitad de mi frecuencia de muestreo.

Equivalentemente, significa que no puedo reconstruir componentes frecuenciales superiores a la mitad de la frecuencia de muestreo, que es exactamente lo que queríamos demostrar.

Aliasing

¿Pensabais que esto había terminado aquí? Aún falta un poquito. Ahora toca hablar de otra consecuencia, menos conocida y mucho peor entendida del teorema de muestreo, el terrible y horrible Aliasing.

Siento deciros que os he mentido media entrada. ¿Recordáis que os he dicho que sólo os voy a dar el componente de menor frecuencia? Pues es mentira, siempre os voy a dar los de ambos sentidos de giro.

Recordáis el primer ejemplo del fasor, donde era muy sencillo determinar la frecuencia. Vamos a pintarlo en junto a su espectro.

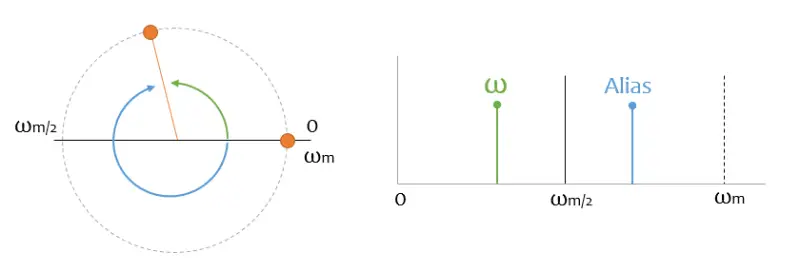
En realidad no voy a tener solo pico verde, si no que voy a tener también uno azul, que corresponden con la frecuencia girando en el otro sentido. Esta señal “espejo” se denomina “alias”, y es la que da origen al fenómeno de Aliasing.

Este pico no parece muy problemático, porque está por encima de la mitad de la frecuencia de muestreo. Y, cómo somos chicos listos, y gracias al genio de Nyquist y Shannon, sé que todo lo que hay por encima es “garbage” y no pienso ni mirarlo al reconstruir la señal.

Ojalá fuera tan fácil. Pero mirar lo que pasa con un ruido “algo superior” a la mitad de la frecuencia de muestreo, que me aparece como una frecuencia alta en mi señal digital muestreada ¡Y no puedo distinguirlo de los datos “de verdad”!

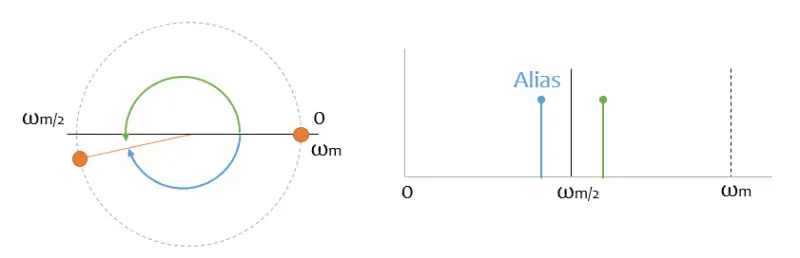
Es incluso peor si se acerca a la señal de muestreo, porque me aparece como componentes de baja frecuencia en mi señal digital. Y es peor porque, normalmente, en las frecuencias bajas tengo mucha “chicha” de mi señal.

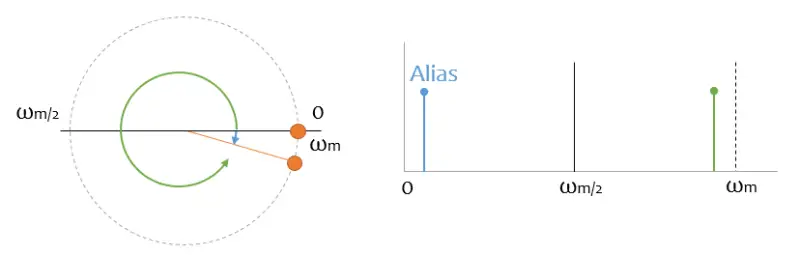
Pero no solo eso, también todos los armónicos de las frecuencias superiores a la mitad de la frecuencia de muestreo me van a generar Aliasing.

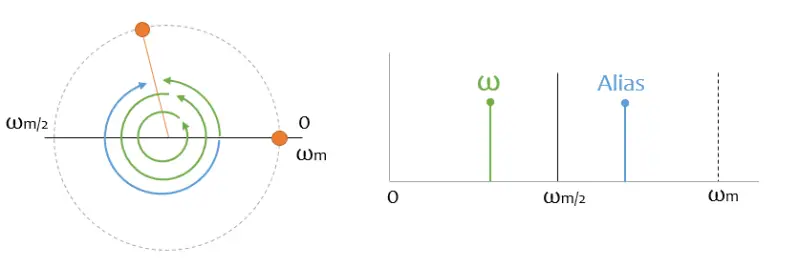
En general, cuando yo hago un proceso de muestreo de una señal, estoy muestreando el “espejo” de todo su espectro y de todos sus armónicos. Y toda esa señal me la estoy “comiendo” y no tengo forma de distinguirlo de los datos de “verdad”

Por eso, siempre siempre siempre, antes de muestrear una señal hay que hacer un filtrado para las bandas superiores a la mitad de la frecuencia de muestreo, para impedir que toda esa información se cuele en el espectro registrado.

Conclusión

¿Un poco largo? Espero que no se os haya hecho muy pesado, y que hayáis visto una forma distinta de entender el teorema de muestreo, sin necesidad de ecuaciones (muy bonitas, por otro lado).

El teorema de muestreo es de aplicación en múltiples campos, típicamente en telecomunicaciones y audio, pero también en muchos otros menos evidentes como el tratamiento de imagen (sí, existen FFT 2D y 3D), osciloscopios, instrumentos de medición, y en cualquier aplicación que suponga manipulación digital de señales.

Así que agradezcamos a los genios de Nyquist, Shannon y otros contribuyentes a la teoría de tratamiento digital de información por su labor y ¡Nos vemos en la próxima entrada!