En esta entrada vamos a ver cómo implementar una red de Petri en un procesador como Arduino. Las redes de Petri son un mecanismo potente en teoría de eventos y, especialmente, en sistemas con eventos concurrentes.
En una entrada anterior vimos las máquinas de estados finitas como una forma estructurada de plantear la programación de un autómata. En cierto modo, podemos considerar las redes de Petri como una evolución de las máquinas de estados.
En una máquina de estados un único puede estar activado en cada momento. Los cambios de estado se realizan a través de transiciones, que dependen únicamente del estado actual y de una condición asociada a la transición.
Por contra en una red de Petri en lugar de tener estados tenemos nodos. Cada nodo puede tener un número nulo o no nulo de marcas. En la representación gráfica de una red de Petri, las marcas suelen representarse como puntos en el interior de los nodos.
Aquí tenemos algunas representaciones gráficas de redes de Petri sencillas.
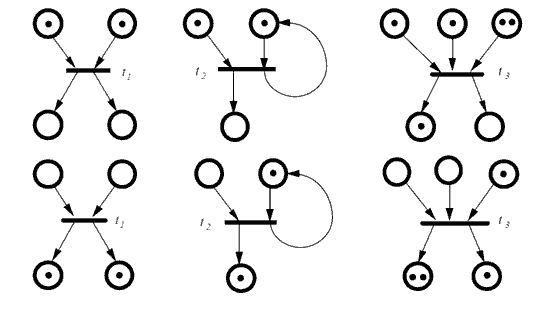
Otra diferencia respecto a una máquina de estados finitos es que las transiciones de una red de Petri pueden estar asociadas a más de un nodo de entrada y tener más de un nodo de salida.
Para que una transición pueda disparar debe, además de cumplir la condición asociada, tener al menos una marca en cada uno de sus nodos de entrada. En este caso decimos que la transición está sensibilizada, lo que significa que puede disparar si se cumple su condición asociada.
Al disparar una transición, esta retira una marca de cada uno de los nodos de entrada y añade una marca a cada nodo de salida.
Las redes de Petri permiten una representación más conveniente de ciertos autómatas, en especial de aquellos que requieren de eventos concurrentes o sincronización de ramas. Imaginemos, por ejemplo, una máquina industrial que para poder realizar una operación necesita que exista una pieza en dos estaciones de trabajo (ejemplo, no puedo montar una botella de zumo hasta que no tenga la botella, el tapón, y la etiqueta).
Ejemplo de red de Petri
El ejemplo clásico para ilustrar el funcionamiento y utilidad de una red de Petri es el caso de dos carros sincronizados. Disponemos de dos railes, por los cuales circulan sendos carros. Al pulsar un botón, el carro del rail superior pasa al otro lado. Otro botón realiza lo mismo con el carro del carril inferior.
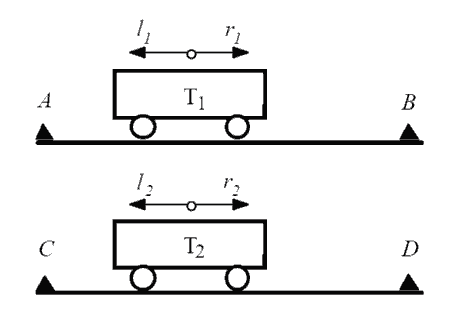
Sin embargo, para que ambos carros puedan moverse se requiere que estos estén sincronizados. Es decir, que ambos carros deben haber cambiado de lado antes de que uno de ellos pueda volver. No es posible, por ejemplo, que el carro superior cambia de estación varias veces mientras el inferior está quieto.
Este problema admite una representación sencilla en forma de red de Petri mientras que, en el caso de realizarlo como máquina de estados, la solución es comparativamente más compleja.
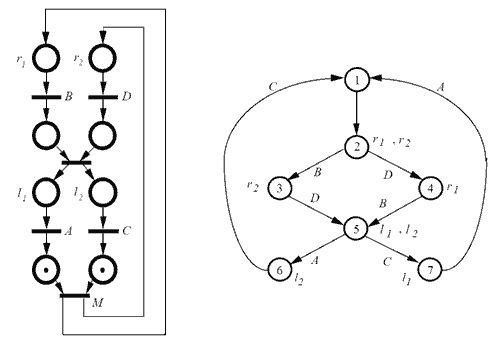
La ventaja de la red de Petri queda patente si, en lugar de dos carros, empleamos tres. La red de Petri sigue siendo sencilla, mientras que vemos que la complejidad necesaria para la máquina de estados equivalente se dispara.
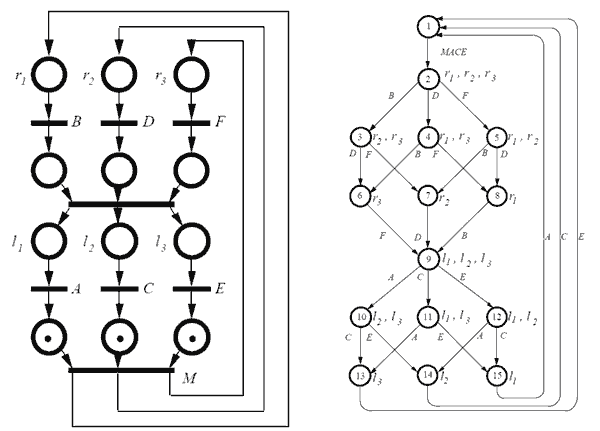
Esto ilustra la conveniencia y utilidad de las redes de Petri respecto a las máquinas de estados finitas, especialmente en el manejo de autómatas con ramas paralelas y necesidad de sincronización de eventos.
Implementar una red de Petri en Arduino
Después de esta pequeña introducción a las redes de Petri, vamos a ver como no es tan difícil como parece realizar una implementación sencilla en Arduino.
Vamos a verlo con un ejemplo sencillo, una variación del ejemplo de los carros sincronizados que hemos dicho anteriormente. Aunque quizás resulta más sencillo de visualizar si imagináis, por ejemplo, que son piezas en una cadena de montaje.
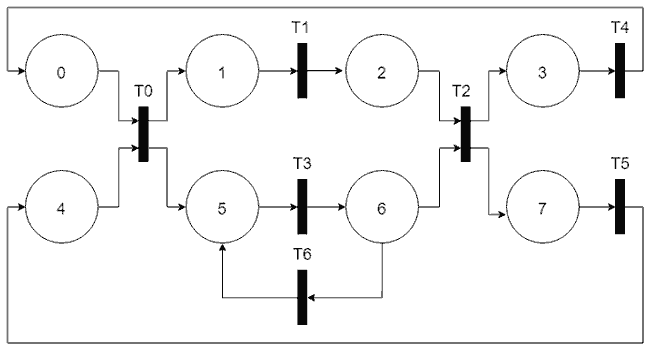
En el ejemplo tenemos dos ramas, inferior y superior, y cuatro estaciones, por lo que tenemos un total de ocho estados. La rama superior avanza cuando recibe por puerto serie el carácter ‘A’ y el inferior cuando recibe ‘B’.
Para que sea más interesante, el paso de la primera estación y a la última estación admite tanto ‘A’ como ‘B’. Con cualquiera de estas entradas las marcas avanzarán simultáneamente en ambas ramas.
Y por meter un temporizador, vamos a suponer que en la estación inferior el carro vuelve del estado 6 al 5, si la pieza del carril superior no ha avanzado tras un plazo de 5 segundos.
Vamos a ver una implementación muy ligera y muy sencilla de esta red de Petri.
enum Input
{
ForwardA = 0,
ForwardB = 1,
Unknown = 2
};
Input input;
const int numStates = 8;
uint8_t _markup[numStates];
uint8_t _prevMarkup[numStates];
// Definicion de las transiciones
void Transition0()
{
if (_prevMarkup[0] && _prevMarkup[4] && (input == Input::ForwardA || input == Input::ForwardB))
{
RemoveMark(0); RemoveMark(4);
AddMark(1); AddMark(5);
Serial.println("Fired T0");
printMarkup();
}
}
void Transition1()
{
if (_prevMarkup[1] && input == Input::ForwardA)
{
RemoveMark(1);
AddMark(2);
Serial.println("Fired T1");
printMarkup();
}
}
void Transition2()
{
if (_prevMarkup[2] && _prevMarkup[6] && (input == Input::ForwardA || input == Input::ForwardB))
{
RemoveMark(2); RemoveMark(6);
AddMark(3); AddMark(7);
Serial.println("Fired T2");
printMarkup();
}
}
void Transition3()
{
if (_prevMarkup[3] && input == Input::ForwardA)
{
RemoveMark(3);
AddMark(0);
Serial.println("Fired T3");
printMarkup();
}
}
void Transition4()
{
if (_prevMarkup[5] && input == Input::ForwardB)
{
RemoveMark(5);
AddMark(6);
activateTimer();
Serial.println("Fired T4");
printMarkup();
}
}
void Transition5()
{
if (_prevMarkup[7] && input == Input::ForwardB)
{
RemoveMark(7);
AddMark(4);
Serial.println("Fired T5");
printMarkup();
}
}
void Transition6()
{
if (_prevMarkup[6] && timerExpired())
{
RemoveMark(6);
AddMark(5);
Serial.println("Fired T6");
printMarkup();
}
}
void setup()
{
Serial.begin(9600);
// Estado inicial
for (uint8_t index = 0; index < numStates; index++)
_markup[index] = 0;
_markup[0] = 1;
_markup[4] = 1;
printMarkup(); // Mostrar el estado inicial
}
void loop()
{
input = static_cast<Input>(readInput());
Update();
}
// Actualizar la red
void Update()
{
// Copiar markup a prevaMarkup
memcpy(_prevMarkup, _markup, numStates * sizeof(uint8_t));
Transition0();
Transition1();
Transition2();
Transition3();
Transition4();
Transition5();
Transition6();
}
void AddMark(uint8_t index)
{
_markup[index]++;
}
void RemoveMark(uint8_t index)
{
_prevMarkup[index]--;
_markup[index]--;
}
// Realiza la lectura de un caracter para el ejemplo
int readInput()
{
Input currentInput = Input::Unknown;
if (Serial.available())
{
char incomingChar = Serial.read();
switch (incomingChar)
{
case 'A': currentInput = Input::ForwardA; break;
case 'B': currentInput = Input::ForwardB; break;
default: break;
}
}
return currentInput;
}
// Para debug del ejemplo
void printMarkup()
{
Serial.print(_markup[0]);
Serial.print(_markup[1]);
Serial.print(_markup[2]);
Serial.println(_markup[3]);
Serial.print(_markup[4]);
Serial.print(_markup[5]);
Serial.print(_markup[6]);
Serial.println(_markup[7]);
}
// Timer para la transicion 6
unsigned long previousMillis;
bool isTimerON = false;
void activateTimer()
{
isTimerON = true;
previousMillis = millis();
}
bool timerExpired()
{
if (isTimerON == false) return false;
if ((unsigned long)(millis() - previousMillis) >= 5000)
return true;
return false;
}En esta implementación sencilla, por un lado, tenemos dos vectores que almacenan el estado de marcaje actual y anterior (luego veremos para que necesitamos el anterior).
La mayor parte del peso del programa está en las funciones Transicion0…5(), que contienen toda la lógica de las transiciones. Comprueban que la transición está sensibilizada, y que se cumple la condición de disparo. En caso de cumplirse la condición, y estar sensibilizada, realiza las acciones oportunas, y actualiza el marcado de la red de Petri.
En la función Setup simplemente iniciamos el estado de las marcas a la posición inicial. En el loop, recibimos un carácter por puerto serie, y actualizamos el estado de la red de Petri con la función Update. La función Update copia el estado de la máquina al vector de estado anterior, y lanza todas las transiciones. El motivo de copiar el estado de la máquina es evitar que durante los cambios de marcado de una iteración se sensibilicen transiciones que no estaban.
Por este mismo motivo, las marcas se añaden mediante la función AddMark y RemoveMark. Ambos cambios se realizan en nuevo marcado. Pero en el marcado anterior, que se emplea para determinar si una entrada está sensibilizada, únicamente las retiramos, no las añadimos.
Para la entrada temporizada, al disparar la transición 4 activamos un temporizador. La transición 6 tiene como condición de disparo el valor de la función timeExpired que, precisamente, devuelve verdadero cuando el timer ha expirado.
Finalmente, tenemos funciones adicionales para que el ejemplo funcione, como son readInput, que recibe la entrada por puerto serie, y printMarkup que muestra el estado de la red para que podemos comprobar el funcionamiento del ejemplo.
Esta implementación es muy sencilla, pero resulta adecuada para ilustrar que implementar una red de Petri no tiene por qué ser tan complejo como parece. Podríamos mejorarla mucho empleando vectores, estructuras, … pero no tiene mucho sentido porque es justo lo que vamos a ver en el siguiente apartado.
Resultados
Si ejecutamos el código anterior podemos ver por puesto serie el resultado. Podemos cambiar el estado pulsando las teclas ‘A’ y ‘B’.
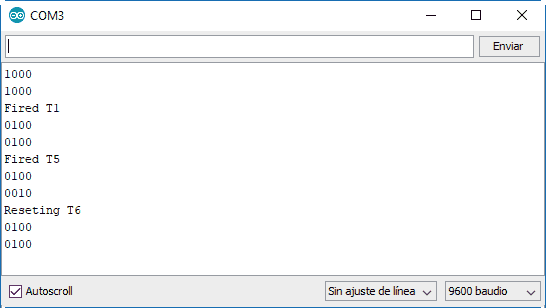
Red de Petri en una librería
Hemos visto una implementación muy sencilla de una Red de Petri en Arduino, de entre las muchas posibles de hacerlo. Pero debería haber quedado claro que tiene grandes partes repetitivas.
En este caso, el código nos está pidiendo a gritos emplear objetos, que en Arduino se traduce en hacer una librería.
Así que aquí tenéis la librería PetriNet, que implementa una red de Petri en Arduino de forma cómoda y sencilla, con optimizaciones adicionales. Estáis invitado a echarle un vistazo al código.
Con esta librería, el ejemplo anterior se resolvería con el siguiente código.
#include "PetriNetLib.h"
enum Input
{
ForwardA = 0,
ForwardB = 1,
Unknown = 2
};
Input input;
PetriNet petriNet(8, 7);
void setup()
{
Serial.begin(9600);
// Definicion de la red de petri del ejemplo
// Entradas y salidas de los estados
static uint8_t inputs0[] = { 0, 4 };
static uint8_t outputs0[] = { 1, 5 };
static uint8_t inputs1[] = { 1 };
static uint8_t outputs1[] = { 2 };
static uint8_t inputs2[] = { 2, 6 };
static uint8_t outputs2[] = { 3, 7 };
static uint8_t inputs3[] = { 3 };
static uint8_t outputs3[] = { 0 };
static uint8_t inputs4[] = { 5 };
static uint8_t outputs4[] = { 6 };
static uint8_t inputs5[] = { 7 };
static uint8_t outputs5[] = { 4 };
// Transiciones
petriNet.SetTransition(0, inputs0, 2, outputs0, 2,
[]() -> bool {return input == Input::ForwardA || input == Input::ForwardB; },
[]() {Serial.println("Fired T0"); printMarkup(); });
petriNet.SetTransition(1, inputs1, 1, outputs1, 1,
[]() -> bool {return input == Input::ForwardA; },
[]() {Serial.println("Fired T1"); printMarkup(); });
petriNet.SetTransition(2, inputs2, 2, outputs2, 2,
[]() -> bool {return input == Input::ForwardA || input == Input::ForwardB; },
[]() {Serial.println("Fired T2"); printMarkup(); });
petriNet.SetTransition(3, inputs3, 1, outputs3, 1,
[]() -> bool {return input == Input::ForwardA; },
[]() {Serial.println("Fired T3"); printMarkup(); });
petriNet.SetTransition(4, inputs4, 1, outputs4, 1,
[]() -> bool {return input == Input::ForwardB; },
[]() {Serial.println("Fired T4"); printMarkup(); activateTimer(); });
petriNet.SetTransition(5, inputs5, 1, outputs5, 1,
[]() -> bool {return input == Input::ForwardB; },
[]() {Serial.println("Fired T5"); printMarkup(); });
petriNet.SetTransition(6, outputs4, 1, inputs4, 1,
timerExpired,
[]() {Serial.println("Reseting T6"); printMarkup(); });
// Marcado inicial
petriNet.SetMarkup(0, 1);
petriNet.SetMarkup(4, 1);
printMarkup(); // Mostrar el estado inicial
}
void loop()
{
input = static_cast<Input>(readInput());
petriNet.Update();
}
// Realiza la lectura de un caracter para el ejemplo
int readInput()
{
Input currentInput = Input::Unknown;
if (Serial.available())
{
char incomingChar = Serial.read();
switch (incomingChar)
{
case 'A': currentInput = Input::ForwardA; break;
case 'B': currentInput = Input::ForwardB; break;
default: break;
}
}
return currentInput;
}
// Para debug del ejemplo
void printMarkup()
{
Serial.print(petriNet.GetMarkup(0));
Serial.print(petriNet.GetMarkup(1));
Serial.print(petriNet.GetMarkup(2));
Serial.println(petriNet.GetMarkup(3));
Serial.print(petriNet.GetMarkup(4));
Serial.print(petriNet.GetMarkup(5));
Serial.print(petriNet.GetMarkup(6));
Serial.println(petriNet.GetMarkup(7));
}
// Timer para la transicion 6
unsigned long previousMillis;
bool isTimerON = false;
void activateTimer()
{
isTimerON = true;
previousMillis = millis();
}
bool timerExpired()
{
if (isTimerON == false) return false;
if ((unsigned long)(millis() - previousMillis) >= 5000)
return true;
return false;
}Descarga el código
Todo el código de esta entrada está disponible para su descarga en Github.