En entradas anteriores hemos visto el funcionamiento de acelerómetros y giroscopios como sensores que pueden ser empleados para determinar la orientación de un dispositivo.
También vimos las ventajas y limitaciones de cada uno de los dispositivos, y adelantamos que se combinan muy bien porque las características de su medición se complementan.
En esta última entrada de la serie veremos los IMU’s, dispositivos que combinan las ventajas de ambos sensores para obtener mejores funcionalidades que la que podríamos obtener usando un acelerómetro o giroscopio independientemente.
En la actualidad su bajo coste ha hecho que sean componentes frecuentes en una gran cantidad de aparatos cotidianos. Existen muchos fabricantes de IMU’s, como Panasonic, Robert Bosch GmbH, InvenSense, Seiko Epson, Sensonor, STMicroelectronics, Freescale Semiconductor, y AnalogDevices.
Nosotros los usaremos frecuentemente en nuestros proyectos de electrónica y Arduino, por ejemplo, para determinar la dirección de avance de un vehículo, la orientación de un accionador, la inclinación de una plataforma, o incluso como forma de actuar con un ordenador con un guante o un ratón 3D.
¿Qué es un IMU?
Una unidad de medición inercial (IMU) es el nombre genérico para denominar a un dispositivo que es capaz de medir la velocidad, orientación y aceleración de un sistema.
En realidad, los acelerómetros y giroscopios pueden ser considerados como IMU’s simples pero, en general, el nombre de IMU se reserva para dispositivos que integran más de un sistema de medición.
Al hablar de IMU’s es frecuente hacer referencia a la cantidad de grados de libertad (DOF) que dispone. Los grados de libertad de un sensor representan la cantidad de magnitudes independientes que es capaz de medir.
Así, un acelerómetro de 3 ejes ortogonales es un sensor de 3 DOF. Así mismo, un giroscopio que mida ángulos en 3 ejes ortogonales es un sensor de 3DOF.
Los IMU’s que encontraremos más frecuentemente son:
- IMU de 6 DOF, combinando un acelerómetro de 3 ejes y un giroscopio de 3 ejes.
- IMU de 9 DOF, añadiendo una brújula magnética de 3 ejes.
- IMU de 10 DOF, que añade un barómetro para la estimación de la altura del sensor.
Como vemos, la mayoría de los IMU’s parten de una combinación de acelerómetro y giroscopio, siendo este el IMU más habitual. El motivo es que ambos dispositivos combinan muy bien y compensan las limitaciones del otro.
- Los acelerómetros no tienen deriva (drift) a medio o largo plazo, ya que realizan la medición medida absoluta del ángulo que forma el sensor con la dirección vertical, marcada por la gravedad. Sin embargo, se ven influenciados por los movimientos del sensor y el ruido por lo que no son fiables a corto plazo.
- Los giroscopios funcionan muy bien para movimientos cortos o bruscos, pero al usar giroscopios de vibración que realmente miden la velocidad angular, y obtienen el ángulo por integración respecto al tiempo, acumulan los errores y el ruido en la medición, por lo que a medio o largo plazo tienen deriva (drift).
Por tanto combinar las mediciones de ambos dispositivos permite a las IMU obtener mediciones de la orientación más precisas que la de un acelerómetro y un giroscopio por separado (veremos esto a continuación, pero antes haremos una reflexión sobre que es la orientación).
Obtener la orientación con un IMU
Para determinar la distribución de un objeto respecto a una base en un espacio tridimensional deberemos establecer su posición y orientación. Se requieren tres parámetros para determinar la posición relativa y otros tres para determinar su orientación.
En la vida cotidiana estamos acostumbrados a tratar la posición de un objeto, y sabemos que existe más de una forma de expresar su posición relativa matemáticamente. Por ejemplo, podemos expresar sus coordenadas respecto en otra base, mediante coordenadas cartesianas (X, Y, Z), cilíndricas o esféricas.
Sin embargo, no estamos tan acostumbrados a trabajar con la parametrización de la orientación, ya que matemáticamente es algo más compleja. Al igual que la posición, existe más de una forma de expresar la orientación relativa de dos sistemas (como por ejemplo los ángulos de Euler, las matrices de rotación o los cuaterniones)
Seguramente la más extendida e intuitiva son los ángulos de navegación, o ángulos de Tait-Bryan, en los que la orientación se representa como tres rotaciones ortogonales en torno al eje X (roll), Y (pitch), y Z (yaw).
Los ángulos de Tait-Bryan son una variación de los ángulos de Euler, introducidos por el matemático Leonhard Euler durante su estudio sobre la mecánica del sólido rígido.
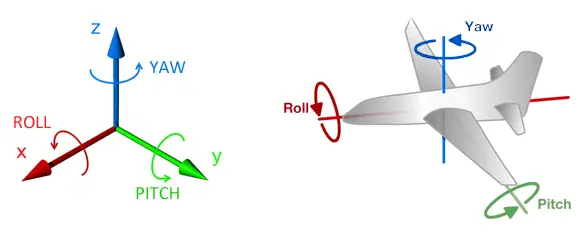
Es frecuente encontrar incorrectamente los ángulos de Tait-Brayn denominados como ángulos de Euler. Los ángulos de Euler son una formulación más general. Otra diferencia es que los ángulos de Euler toman como origen de la medición la vertical, mientras que Tait-Brayn mide los ángulos respecto a la horizontal.
Los ángulos ángulos de Tait-Bryan son intuitivos y sencillos. Además tienen la ventaja de ser conmutativos, es decir, la orientación final obtenida es independiente de orden en el que apliquemos la rotación (algo que en normalmente no ocurre en la representación de rotaciones).
Sin embargo, adolecen de una gran desventaja denominada bloqueo cardán (gimbal lock) que sufren todos los sistemas de ángulos de Euler. Cuando el eje Y gira +-90º, el eje X y el Z coinciden por lo que el sistema degenera a 2DOF, lo cuál da lugar a un punto singular no diferenciable que puede suponer problemas de estabilidad en los cálculos.
El gimbal lock es una desventaja tan importante que la forma habitual de representar la rotación mediante el uso de cuaterinones. Los cuaterniones son una extensión de los números complejos introducida por Hamilton en 1843, que emplean tres unidades imaginarias i, j, y k tal que,
Es sabido que números complejos pueden usarse para representar vectores en el plano. De forma equivalente, un cuaternión permite expresar un vector en el espacio tridimensional.
Para expresar la rotación de un punto, un ángulo α, en torno a un vector arbitrario de coordenadas Ex, Ey, Ez, el cuaternión resultante adopta la siguiente expresión
Comparados con los ángulos de Euler, los cuaterniones son más simples de componer y evitan el problema del bloqueo del cardán. Comparados con las matrices de rotación, son más eficientes y más estables numéricamente
Por este motivo los cuaterniones son una de las formas más habituales de expresar la orientación en gráficos de ordenador y serán la forma preferida a emplear cuando queramos trabajar con orientaciones en IMU’s y en proyectos de Arduino.
Filtrado de señal en un IMU
Para poder tener las ventajas en tiempos cortos del giroscopio y las ventajas a medio y largo plazo del acelerómetro es necesario que combinemos y filtremos la señal registrada en bruto (RAW).
Existen varios filtros posibles siendo el más famoso el filtro de Kalman, desarrollado en 1960 por Rudolf E. Kalman. Es considerado como uno de los grandes descubrimientos del siglo XX por sus implicaciones en el proceso de filtrado en sensores (no solo IMU’s) y es uno de artífices de la carrera espacial.
A grandes rasgos el filtro de Kalman realiza una estimación del valor futuro de la medición, y después compara el valor real mediante un análisis estadístico para compensar el error en futuras mediciones.
Sin embargo, el filtro de Kalman en su versión general implica la realización de cálculos complejos (ver Wikipedia) que suponen una implementación y tiempo de cálculo excesivo para Arduino.
Por este motivo es frecuente emplear un filtro más sencillo denominado filtro complementario. En realidad, el filtro complementario puede considerarse una simplificación del filtro de Kalman que prescinde por completo del análisis estadístico.
Existen varias formulaciones para un filtro complementario. En su expresión más sencilla, el filtro complementario puede expresarse.
Donde A y B son dos constantes que, inicialmente, puede tomarse 0.98 y 0.02 respectivamente. Podemos calibrar el filtro simplemente variando los valores de A y B siempre que cumplamos la condición de que sumen 1 entre ellos.
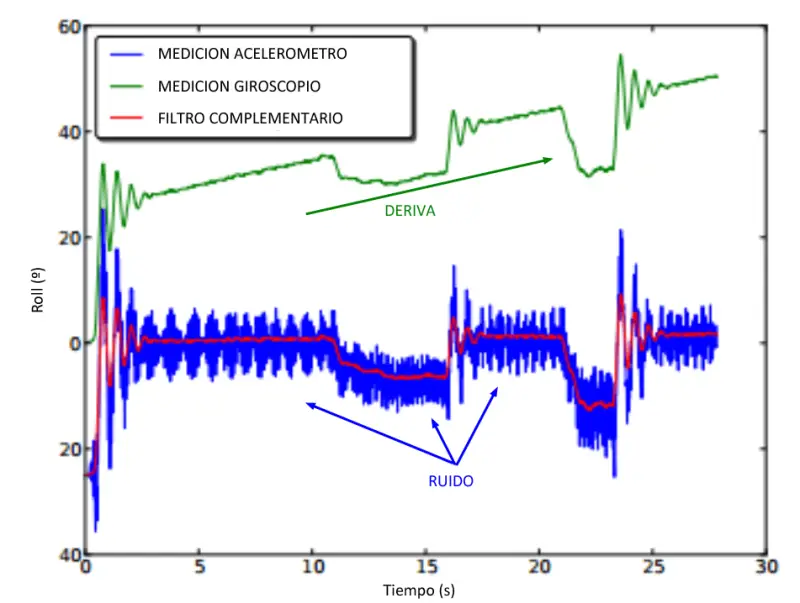
El filtro complementario se comporta como un filtro de paso alto para la medición del giroscopio y un filtro de paso bajo para la señal del acelerómetro. Es decir, la señal del giroscopio manda a corto plazo, y la del acelerómetro y medio y largo, que es exactamente lo que queremos para compensar sus ventajas y defectos.
En la mayoría de aplicaciones domésticas, el filtro complementario es suficiente y proporciona valores muy similares al filtro Kalman, siempre que los valores de A y B estén debidamente calibrados.
Existen versiones más sofisticadas del filtro complementario, así como versiones simplificadas unidimensionales del filtro de Kalman que sí pueden ser implementadas en Arduino. Veremos esto en una próxima entrada avanzada.
Mientras tanto, emplearemos las IMU’s como el MPU6050 y los filtros empleados en nuestros proyectos de electrónica y Arduino.
