En esta entrada vamos a ver las ecuaciones necesarias para calcular un robot articulado en un procesador como Arduino. Y al final ¡veremos una librería para que no tengáis que hacerlo nunca más!
La resolución de la posición y ángulos de polígonos articulados, en especial triángulos y cuadriláteros, resulta importante porque aparece frecuentemente al trabajar con robots articulados, como en el caso de brazos robóticos, cuadrípedos, hexápodos, bípedos, etc.
En general, en los robots articulados sabemos la distancia de cada uno de los lados del polígono articulado y actuamos sobre los motores para variar el ángulo que forman entre ellas.
También conocemos las coordenadas del punto inicial del polígono (o bien no nos importan, si vamos a usar coordenadas relativas al mismo). Por su parte, cada nodo de la articulación tiene sus propias coordenadas, teniendo especialmente interés en el “punto final” porque normalmente es donde tendremos el efector (la pinza del brazo, la pata del robot, etc).
Con esto, tenemos dos tipos de cálculos que aparecen en la resolución de robots articulados:
- Directo, donde sabemos los ángulos de las articulaciones, y queremos saber la posición del efector.
- Inverso, donde sabemos la posición del efector, y queremos calcular los ángulos necesarios para conseguirlo.
Siendo más frecuente en robots articulados el último de estos dos. Por ejemplo, sabemos donde esta la pelota que queremos coger o donde queremos poner una pata, y necesitamos saber qué ángulos fijar en los motores para conseguirlo.
El cálculo no es especialmente complicado, pero requiere de una pequeña dosis de trigonometría. Por otro lado, destacar que no todas las posiciones van a tener resolución, mientras que por el contrario algunas van a tener más de una (en general, infinitas) soluciones posibles.
Sin más, vamos a ver cómo resolver este problema para el caso de triángulos y cuadriláteros articulados en 2D, y 3D, los casos más frecuentes que tendremos al trabajar con robots articulados.
Triángulo articulado 2D
Directo
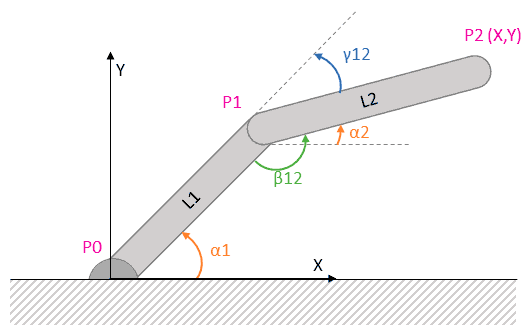
El cálculo directo de la posición del efectos (P2), en función de los ángulos absolutos de los segmentos se obtiene simplemente proyectando en X e Y, de la siguiente forma.
Donde la relación entre los ángulos relativos entre los segmentos (tanto interior, como exterior) y los ángulos absolutos de los mismos se calculan mediante las siguientes expresiones
Inverso
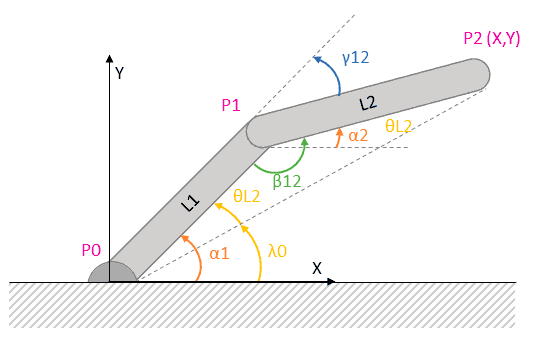
El cálculo inverso, es igualmente sencillo, considerando que los dos segmentos forman un triángulo junto con la línea imaginaría que unen P0 y P2.
Podemos calcular distancia D desde la base P0 a P2, aplicando el teorema de Pitágoras.
Con esta distancia y las longitudes de los segmentos podemos calcular todos los ángulos interiores del triángulo aplicando el teorema del coseno generalizado.
Por otro lado, podemos calcular el ángulo que forma el triángulo respecto al eje X con la siguiente expresión.
Finalmente, calculamos el ángulo absoluto del primer segmento haciendo.
Conocido el ángulo absoluto del primer segmento y el ángulo relativo entre los mismos, podemos calcular el resto de ángulos relativos y absolutos usando las expresiones que hemos visto con anterioridad.
Lógicamente, no todas las posiciones admiten una solución, como por ejemplo las que excedan el alcance de los brazos.
Código
Así sería un posible ejemplo de código para resolver un triángulo articulado en 2D en un procesador como Arduino.
float L1, L2, D;
float AbsoluteAngle1, AbsoluteAngle2;
float RelativeAngle12;
float TargetX, TargetY;
float Pythagoras(const float& x, const float& y)
{
const float d = sqrt(x * x + y * y);
return d;
}
float SolveInverseCosine(const float& l1, const float& l2, const float& l3)
{
const float angle3 = acos((l1 * l1 + l2 * l2 - l3 * l3) / (2 * l1 * l2));
return angle3;
}
float AbsoluteToRelative(float absolute1, float absolute2)
{
return absolute2 - absolute1 + PI;
}
float RelativeToAbsolute(float relative12, float absolute1)
{
return absolute1 + relative12 - PI;
}
void SolveTriangle(float& x, float& y, float& l1, float& l2, float& d, float& absoluteAngle1, float& absoluteAngle2, float& relativeAngle12)
{
const float angle_0 = atan2(y, x);
d = Pythagoras(x, y);
const float angle_l1 = SolveInverseCosine(d, l2, l1);
const float angle_l2 = SolveInverseCosine(d, l1, l2);
const float angle_D = PI - angle_l1 - angle_l2;
absoluteAngle1 = angle_0 + angle_l2;
relativeAngle12 = angle_D;
absoluteAngle2 = RelativeToAbsolute(relativeAngle12, absoluteAngle1);
}
void SolveDirect(float angle1, float angle2)
{
AbsoluteAngle1 = angle1;
AbsoluteAngle2 = angle2;
SolveDirect();
}
void SolveDirect()
{
RelativeAngle12 = AbsoluteToRelative(AbsoluteAngle1, AbsoluteAngle2);
TargetX = L1 * cos(AbsoluteAngle1) + L2 * cos(AbsoluteAngle2);
TargetY = L1 * sin(AbsoluteAngle1) + L2 * sin(AbsoluteAngle2);
D = Pythagoras(TargetX, TargetY);
}
void SolveReverse()
{
D = Pythagoras(TargetX, TargetY);
float P2x = TargetX;
float P2y = TargetY;
float D0;
SolveTriangle(P2x, P2y, L1, L2, D0, AbsoluteAngle1, AbsoluteAngle2, RelativeAngle12);
}
void Debug()
{
Serial.print(F("Target X:\t"));
Serial.println(TargetX, 4);
Serial.print(F("Target Y:\t"));
Serial.println(TargetY, 4);
Serial.print(F("Abs. Angle 1:\t"));
Serial.println(degrees(AbsoluteAngle1), 4);
Serial.print(F("Abs. Angle 2:\t"));
Serial.println(degrees(AbsoluteAngle2), 4);
Serial.print(F("Rel. Angle 12:\t"));
Serial.println(degrees(RelativeAngle12), 4);
}
void setup()
{
Serial.begin(115200);
while (!Serial) { ; }
L1 = 100; L2 = 50;
Serial.println(F("Solve Direct Relative"));
SolveDirect(radians(55), radians(-20));
Debug();
Serial.println(F("Solve Inverse"));
TargetX = 104.3423;
TargetY = 64.8141;
SolveReverse();
Debug();
}
void loop()
{
// Do nothing
delay(10000);
}Cuadrilátero articulado 2D
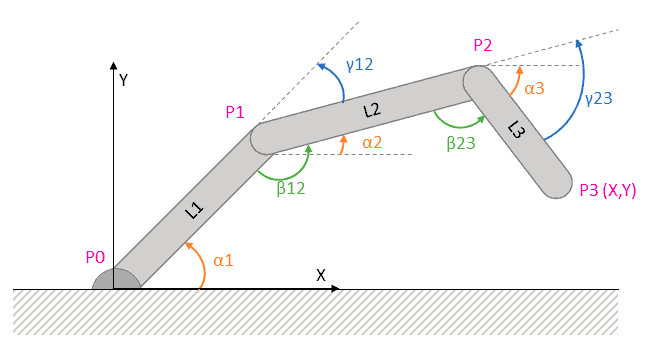
Directo
La resolución de un cuadrilátero articulado es similar al triángulo articulado, simplemente proyectamos el nuevo segmento en los ejes X e Y.
Inverso
La resolución de un cuadrilátero articulado no es más compleja que la del triángulo en 2D. El nuevo segmento añade un grado de libertad adicional por lo que, en general, el problema admite múltiples soluciones (infinitas).
Para poder resolver el sistema debemos imponer una condición (o relación entre condiciones). Lo habitual es proporcionar el ángulo absoluto del ultimo segmento, que corresponde con el angulo de ataque del efector.
Con las coordenadas del punto P2, resolveríamos como en el caso anterior. Igual que en el caso del triángulo, no todas las posiciones admiten solución. Por otro lado, es posible que exista solución solo para un cierto rango de valores de ángulo del efector.
Con frecuencia, se establece una relación entre la posición del efector y su ángulo alpha_3, basado en que la variación del ángulo durante el recorrido del robot sea “suave”.
Código
Así sería un posible ejemplo de código para resolver un cuadrilátero articulado en 2D en un procesador como Arduino.
float L1, L2, L3, D;
float AbsoluteAngle1, AbsoluteAngle2, AbsoluteAngle3;
float RelativeAngle12, RelativeAngle23;
float TargetX, TargetY;
float Pythagoras(const float& x, const float& y)
{
const float d = sqrt(x * x + y * y);
return d;
}
float SolveInverseCosine(const float& l1, const float& l2, const float& l3)
{
const float angle3 = acos((l1 * l1 + l2 * l2 - l3 * l3) / (2 * l1 * l2));
return angle3;
}
float AbsoluteToRelative(float absolute1, float absolute2)
{
return absolute2 - absolute1 + PI;
}
float RelativeToAbsolute(float relative12, float absolute1)
{
return absolute1 + relative12 - PI;
}
void SolveTriangle(float& x, float& y, float& l1, float& l2, float& d, float& absoluteAngle1, float& absoluteAngle2, float& relativeAngle12)
{
const float angle_0 = atan2(y, x);
d = Pythagoras(x, y);
const float angle_l1 = SolveInverseCosine(d, l2, l1);
const float angle_l2 = SolveInverseCosine(d, l1, l2);
const float angle_D = PI - angle_l1 - angle_l2;
absoluteAngle1 = angle_0 + angle_l2;
relativeAngle12 = angle_D;
absoluteAngle2 = RelativeToAbsolute(relativeAngle12, absoluteAngle1);
}
void SolveDirect(float angle1, float angle2, float angle3)
{
AbsoluteAngle1 = angle1;
AbsoluteAngle2 = angle2;
AbsoluteAngle3 = angle3;
SolveDirect();
}
void SolveDirect()
{
RelativeAngle12 = AbsoluteToRelative(AbsoluteAngle1, AbsoluteAngle2);
RelativeAngle23 = AbsoluteToRelative(AbsoluteAngle2, AbsoluteAngle3);
TargetX = L1 * cos(AbsoluteAngle1) + L2 * cos(AbsoluteAngle2) + L3 * cos(AbsoluteAngle3);
TargetY = L1 * sin(AbsoluteAngle1) + L2 * sin(AbsoluteAngle2) + L3 * sin(AbsoluteAngle3);
D = Pythagoras(TargetX, TargetY);
}
void SolveReverse(float absoluteAngle3)
{
AbsoluteAngle3 = absoluteAngle3;
D = Pythagoras(TargetX, TargetY);
float P2x = TargetX - L3 * cos(AbsoluteAngle3);
float P2y = TargetY - L3 * sin(AbsoluteAngle3);
float D0;
SolveTriangle(P2x, P2y, L1, L2, D0, AbsoluteAngle1, AbsoluteAngle2, RelativeAngle12);
RelativeAngle23 = AbsoluteToRelative(AbsoluteAngle2, AbsoluteAngle3);
}
void Debug()
{
Serial.print(F("Target X:\t"));
Serial.println(TargetX, 4);
Serial.print(F("Target Y:\t"));
Serial.println(TargetY, 4);
Serial.print(F("Abs. Angle 1:\t"));
Serial.println(degrees(AbsoluteAngle1), 4);
Serial.print(F("Abs. Angle 2:\t"));
Serial.println(degrees(AbsoluteAngle2), 4);
Serial.print(F("Abs. Angle 3:\t"));
Serial.println(degrees(AbsoluteAngle3), 4);
Serial.print(F("Rel. Angle 12:\t"));
Serial.println(degrees(RelativeAngle12), 4);
Serial.print(F("Rel. Angle 23:\t"));
Serial.println(degrees(RelativeAngle23), 4);
}
void setup()
{
Serial.begin(115200);
while (!Serial) { ; }
L1 = 100; L2 = 50; L3 = 30;
Serial.println(F("Solve Direct Relative"));
SolveDirect(radians(55), radians(-20), radians(-70));
Debug();
Serial.println(F("Solve Inverse"));
TargetX = 114.60289;
TargetY = 36.62342;
SolveReverse(radians(-70));
Debug();
}
void loop()
{
// Do nothing
delay(10000);
}Triángulo articulado 3D
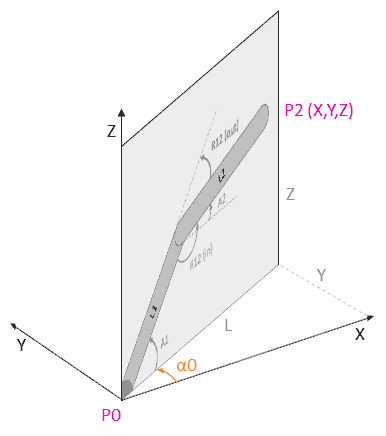
Directo
El caso de un polígono articulado en 3D puede resolverse con las mismas herramientas que en el caso 2D, simplemente considerando que ocurren en un plano girado un ángulo alpha_0 respecto al eje Z.
Para convertir las coordenadas de cualquier punto calculado en el plano (Pn’) a sus equivalentes en 3D (Pn) usamos las siguientes relaciones.
Siendo sigma el ángulo de rotación entre el plano y el eje X.
Inverso
De forma similar, podremos convertir el cálculo inverso de un triángulo en 3D a un caso en 2D proyectando en el plano equivalente.
Para ello, llevaremos las coordenadas 3D del efector (P2) a su equivalente en 2D (P2’) mediante la siguientes relaciones.
Finalmente, resolveríamos como en el caso 2D. Los ángulos entre segmentos calculados son los mismos que en el caso 3D. Si quisiéramos calcular coordenadas de puntos, usaríamos las relaciones anterior para pasar de 2D a 3D.
Código
Así sería un posible ejemplo de código para resolver un triángulo articulado en 3D en un procesador como Arduino.
float L1, L2, D;
float AbsoluteAngle0, AbsoluteAngle1, AbsoluteAngle2;
float RelativeAngle12;
float TargetX, TargetY, TargetZ;
float Pythagoras(const float& x, const float& y)
{
const float d = sqrt(x * x + y * y);
return d;
}
float Pythagoras(const float& x, const float& y, const float& z)
{
const float d = sqrt(x * x + y * y + z * z);
return d;
}
float SolveInverseCosine(const float& l1, const float& l2, const float& l3)
{
const float angle3 = acos((l1 * l1 + l2 * l2 - l3 * l3) / (2 * l1 * l2));
return angle3;
}
float AbsoluteToRelative(float absolute1, float absolute2)
{
return absolute2 - absolute1 + PI;
}
float RelativeToAbsolute(float relative12, float absolute1)
{
return absolute1 + relative12 - PI;
}
void SolveTriangle(float& x, float& y, float& l1, float& l2, float& d, float& absoluteAngle1, float& absoluteAngle2, float& relativeAngle12)
{
const float angle_0 = atan2(y, x);
d = Pythagoras(x, y);
const float angle_l1 = SolveInverseCosine(d, l2, l1);
const float angle_l2 = SolveInverseCosine(d, l1, l2);
const float angle_D = PI - angle_l1 - angle_l2;
absoluteAngle1 = angle_0 + angle_l2;
relativeAngle12 = angle_D;
absoluteAngle2 = RelativeToAbsolute(relativeAngle12, absoluteAngle1);
}
void SolveDirect(float angle0, float angle1, float angle2)
{
AbsoluteAngle0 = angle0;
AbsoluteAngle1 = angle1;
AbsoluteAngle2 = angle2;
SolveDirect();
}
void SolveDirect()
{
RelativeAngle12 = AbsoluteToRelative(AbsoluteAngle1, AbsoluteAngle2);
float L = L1 * cos(AbsoluteAngle1) + L2 * cos(AbsoluteAngle2);
TargetX = L * cos(AbsoluteAngle0);
TargetY = L * sin(AbsoluteAngle0);
TargetZ = L1 * sin(AbsoluteAngle1) + L2 * sin(AbsoluteAngle2);
D = Pythagoras(TargetX, TargetY, TargetZ);
}
void SolveReverse()
{
AbsoluteAngle0 = atan2(TargetY, TargetX);
D = Pythagoras(TargetX, TargetY, TargetZ);
float Lx = Pythagoras(TargetX, TargetY);
float P2x = Lx;
float P2y = TargetZ;
float D0;
SolveTriangle(P2x, P2y, L1, L2, D0, AbsoluteAngle1, AbsoluteAngle2, RelativeAngle12);
}
void Debug()
{
Serial.print(F("Target X:\t"));
Serial.println(TargetX, 4);
Serial.print(F("Target Y:\t"));
Serial.println(TargetY, 4);
Serial.print(F("Target Z:\t"));
Serial.println(TargetZ, 4);
Serial.print(F("Abs. Angle 0:\t"));
Serial.println(degrees(AbsoluteAngle0), 4);
Serial.print(F("Abs. Angle 1:\t"));
Serial.println(degrees(AbsoluteAngle1), 4);
Serial.print(F("Abs. Angle 2:\t"));
Serial.println(degrees(AbsoluteAngle2), 4);
Serial.print(F("Rel. Angle 12:\t"));
Serial.println(degrees(RelativeAngle12), 4);
}
void setup()
{
Serial.begin(115200);
while (!Serial) { ; }
L1 = 100; L2 = 50;
Serial.println(F("Solve Direct Relative"));
SolveDirect(radians(30), radians(55), radians(-20));
Debug();
Serial.println(F("Solve Inverse"));
TargetX = 90.3631;
TargetY = 52.1711;
TargetZ = 64.8142;
SolveReverse();
Debug();
}
void loop()
{
// Do nothing
delay(10000);
}Cuadrilátero articulado 3D
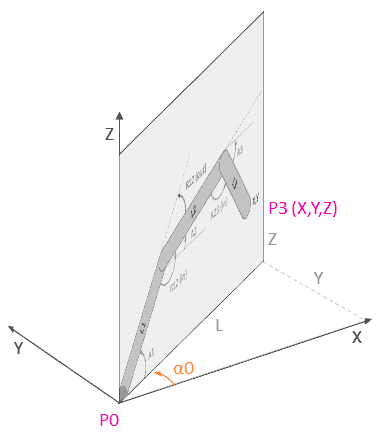
Directo
Análogamente, para el calculo directo de un cuadrilátero articulado en 3D proyectamos igualmente en un plano 2D usando las expresiones del apartado anterior, únicamente considerando que el ángulo alpha_0 esta vez es.
Inverso
Igualmente, un cuadrilátero articulado puede resolverse con las mismas herramientas que su equivalente en 2D. La única diferencia es que, en esta ocasión, las coordenadas del efectos en el caso equivalente en 2D (P3’) se calculan a partir del punto 3D (P3) según la siguiente relación.
Código
Así sería un posible ejemplo de código para resolver un cuadrilátero articulado en 3D en un procesador como Arduino.
float L1, L2, L3, D;
float AbsoluteAngle0, AbsoluteAngle1, AbsoluteAngle2, AbsoluteAngle3;
float RelativeAngle12, RelativeAngle23;
float TargetX, TargetY, TargetZ;
float Pythagoras(const float& x, const float& y)
{
const float d = sqrt(x * x + y * y);
return d;
}
float Pythagoras(const float& x, const float& y, const float& z)
{
const float d = sqrt(x * x + y * y + z * z);
return d;
}
float SolveInverseCosine(const float& l1, const float& l2, const float& l3)
{
const float angle3 = acos((l1 * l1 + l2 * l2 - l3 * l3) / (2 * l1 * l2));
return angle3;
}
float AbsoluteToRelative(float absolute1, float absolute2)
{
return absolute2 - absolute1 + PI;
}
float RelativeToAbsolute(float relative12, float absolute1)
{
return absolute1 + relative12 - PI;
}
void SolveTriangle(float& x, float& y, float& l1, float& l2, float& d, float& absoluteAngle1, float& absoluteAngle2, float& relativeAngle12)
{
const float angle_0 = atan2(y, x);
d = Pythagoras(x, y);
const float angle_l1 = SolveInverseCosine(d, l2, l1);
const float angle_l2 = SolveInverseCosine(d, l1, l2);
const float angle_D = PI - angle_l1 - angle_l2;
absoluteAngle1 = angle_0 + angle_l2;
relativeAngle12 = angle_D;
absoluteAngle2 = RelativeToAbsolute(relativeAngle12, absoluteAngle1);
}
void SolveDirect(float angle0, float angle1, float angle2, float angle3)
{
AbsoluteAngle0 = angle0;
AbsoluteAngle1 = angle1;
AbsoluteAngle2 = angle2;
AbsoluteAngle3 = angle3;
SolveDirect();
}
void SolveDirect()
{
RelativeAngle12 = AbsoluteToRelative(AbsoluteAngle1, AbsoluteAngle2);
RelativeAngle23 = AbsoluteToRelative(AbsoluteAngle2, AbsoluteAngle3);
float L = L1 * cos(AbsoluteAngle1) + L2 * cos(AbsoluteAngle2) + L3 * cos(AbsoluteAngle3);
TargetX = L * cos(AbsoluteAngle0);
TargetY = L * sin(AbsoluteAngle0);
TargetZ = L1 * sin(AbsoluteAngle1) + L2 * sin(AbsoluteAngle2) + L3 * sin(AbsoluteAngle3);
D = Pythagoras(TargetX, TargetY, TargetZ);
}
void SolveReverse(float absoluteAngle3)
{
AbsoluteAngle3 = absoluteAngle3;
AbsoluteAngle0 = atan2(TargetY, TargetX);
D = Pythagoras(TargetX, TargetY, TargetZ);
float Lx = Pythagoras(TargetX, TargetY);
float P2x = Lx - L3 * cos(AbsoluteAngle3);
float P2y = TargetZ - L3 * sin(AbsoluteAngle3);
float D0;
SolveTriangle(P2x, P2y, L1, L2, D0, AbsoluteAngle1, AbsoluteAngle2, RelativeAngle12);
RelativeAngle23 = AbsoluteToRelative(AbsoluteAngle2, AbsoluteAngle3);
}
void Debug()
{
Serial.print(F("Target X:\t"));
Serial.println(TargetX, 4);
Serial.print(F("Target Y:\t"));
Serial.println(TargetY, 4);
Serial.print(F("Target Z:\t"));
Serial.println(TargetZ, 4);
Serial.print(F("Abs. Angle 0:\t"));
Serial.println(degrees(AbsoluteAngle0), 4);
Serial.print(F("Abs. Angle 1:\t"));
Serial.println(degrees(AbsoluteAngle1), 4);
Serial.print(F("Abs. Angle 2:\t"));
Serial.println(degrees(AbsoluteAngle2), 4);
Serial.print(F("Abs. Angle 3:\t"));
Serial.println(degrees(AbsoluteAngle3), 4);
Serial.print(F("Rel. Angle 12:\t"));
Serial.println(degrees(RelativeAngle12), 4);
Serial.print(F("Rel. Angle 23:\t"));
Serial.println(degrees(RelativeAngle23), 4);
}
void setup()
{
Serial.begin(115200);
while (!Serial) { ; }
L1 = 100; L2 = 50; L3 = 30;
Serial.println(F("Solve Direct Relative"));
SolveDirect(radians(30), radians(55), radians(-20), radians(-70));
Debug();
Serial.println(F("Solve Inverse"));
TargetX = 99.2490;
TargetY = 57.3014;
TargetZ = 36.62342;
SolveReverse(radians(-70));
Debug();
}
void loop()
{
// Do nothing
delay(10000);
}Librería de Arduino Articulated
¿Y si lo metemos en una librería para que sea más cómodo de usar? Por supuesto que sí, aquí una librería de Articulated para Arduino, que realiza todos los cálculos anteriores de forma cómoda y sencilla. A disfrutarlo!